|
 Things you need to remember about equations and graphs of straight lines: Things you need to remember about equations and graphs of straight lines:
| A linear equation is an equation whose solutions form a straight line on the coordinate plane (on a graph). (Linear = Line) |
Slope formula based on coordinates:
(Slope is represented by "m")
|
Points on Lines:
If a point lies on a line, the coordinates of the point make the equation true.
• Does (4,7) lie on the line y = 3x - 5?
Yes. 7 = 3(4) - 5
7 = 12 - 5
7 = 7 True. |
With the exception of vertical lines,
the graphs of linear equations form functions,
where each x-value corresponds to only one y-value. |
Different Ways to Write Equations of Lines |
 Slope-Intercept Form:
Slope-Intercept Form: y = m + b (m = slope; b = y-intercept) |
• Use when you know the slope and the y-intercept (where the line crosses the y-axis), or are asked to find the slope and/or y-intercept.
• Be sure your equation starts with "y =" to use this form. You will need to rewrite the equation if it does not start in this manner.
 Find the slope and y-intercept of the equation 4x + 2y = 6. Find the slope and y-intercept of the equation 4x + 2y = 6.
Solution: Rewrite the equation to be "y =": y = -2x + 3
Match your new equation to the form y = m + b
Slope (m) is -2 and y-intercept (b) is +3
 Find the equation of a line whose slope is 5 and y-intercept is (0,-6). Find the equation of a line whose slope is 5 and y-intercept is (0,-6).
Solution: The given information tells us that m = 5 and b = -6
Place these values in the form y = m + b
Equation: y = 5x + (-6) or y = 5x - 6
|
 Point Slope Form: Point Slope Form:
| Point Slope Form: y - y1= m (x - x1) |
m = slope; b = y-intercept;
(x1,y1) = any point on the line |
|
• Use when you know a point on the line and the slope (or can determine the slope).
• Be sure to subtract the coordinates of your point on the line from y and from x.
 Find the equation of a line with a slope of -1 passing through (-4,6). Find the equation of a line with a slope of -1 passing through (-4,6).
Solution: The given information tells us that m = -1 and (x1,y1) = (-4,6)
Substitute into the form y - y1 = m(x - x1): y - 6 = -1(x - (-4))
Simplify: y - 6 = -1(x + 4) or y - 6 = -x - 4 or y = -x + 2 or x + y = 2
(Your problem may specify what the equation should look like when you simplify.)
 Find the equation of a line passing through (4,-8) and (-2,6). Find the equation of a line passing through (4,-8) and (-2,6).
Solution: Find the slope first: 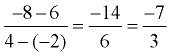
Use either point: we will use (4,-8)
Substitute into the form y - y1 = m(x - x1): 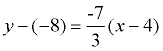
Simplify: 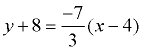 or or 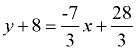 or 3y = -7x + 4 or 7x + 3y = 4 or 3y = -7x + 4 or 7x + 3y = 4
|
 Standard Form: Standard Form:
| Standard Form: Ax + By = C |
A and B cannot both be zero.
|
Different textbooks have different interpretations of the name "standard form", and different statements of the form. You may see Standard Form called General Form. You may see the form written as Ax + By - C = 0. |
|
• Use when asked to place your answer in Standard Form.
 Find the Standard Form equation of a line through (-1,2) and (4,3). Find the Standard Form equation of a line through (-1,2) and (4,3).
Solution: Find the slope first: 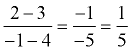
Use either point: we will use (4,3)
Substitute into the form y - y1 = m(x - x1): 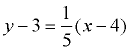
Change to Standard Form: x - 5y = -11
 Find the Standard Form of Find the Standard Form of 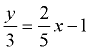 . .
Solution: Multiply All terms by the common denominator, 15. 5y = 6x - 15
Change to Standard Form: 6x - 5y = 15
|
 Horizontal Lines: Horizontal Lines:
Horizontal Line Form: y = 7 (or any number)
|
• Horizontal lines have a slope of zero because they have lots of "run", but no "rise". The rise/run formula always has a numerator of zero, making all of the ratios zero.
• The actual formula is y = 0x + 7, but the 0x is not written.
• This equation describes what is happening to all of the y-coordinates (all y-coordinates are 7).
 Find the equation of a line passing through the points (1,4) and (6,4). Find the equation of a line passing through the points (1,4) and (6,4).
Solution: There are several ways to attack this problem.
If you can picture that plotting these two points will create a horizontal line, your work is easy.
Equation: y = 4
 Find the slope of a horizontal line passing through (-4,-8). Find the slope of a horizontal line passing through (-4,-8).
Solution: All horizontal lines have a slope of zero.
The point (-4,-8) is not needed (it is a distractor).
Slope = 0.
|
 Vertical Lines: Vertical Lines:
Vertical Line Form: x = -3 (or any number)
|
• Vertical lines have no slope (undefined) because they have lots of "rise", but no "run". The rise/run formula always has a denominator of zero, making all of the ratios undefined.
• Vertical line formulas never contain a y-value.
• This equation describes what is happening to all of the x-coordinates (all x-coordinates are -3).
 Find the equation of a line passing through the points (7,4) and (7,-2). Find the equation of a line passing through the points (7,4) and (7,-2).
Solution: There are several ways to attack this problem.
If you can picture that plotting these two points will create a vertical line, your work is easy.
Equation: x = 7
 Find the slope of a vertical line passing through (1,2). Find the slope of a vertical line passing through (1,2).
Solution: All vertical lines have no slope (or undefined slope). The slope does not exist.
The point (1,2) is not needed (it is a distractor).
Slope = undefined (does not exist).
Graphs of vertical lines are never "functions" because the x-value corresponds to an infinite number of y-values. |
 Using the Graphing Calculator: Using the Graphing Calculator:
While the graphing calculator can be helpful in working with any of the methods shown above, the calculator can also create the equation of a line given two points on the line. The calculator uses a statistics feature called a "Linear Regression" to give you the slope and y-intercept of y = ax + b (the calculator's version of y = mx + b). Follow the link below to see how this works.
|
For calculator help with Creating Equations
click here. |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|