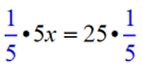|
When you solve an equation, you use a process called deductive reasoning where you apply ideas that you know to be true. For example, you know that if you add the same number to both sides of an equation, the equation will not be changed. Many of the "ideas" that you use when solving are, in actuality, the mathematical properties (rules) that we saw in Real Numbers and Properties.
| |
Using real number properties
(such as the commutative, associative, and distributive properties)
and the properties of equality
(such as adding, subtracting, multiplying and dividing by a non-zero) |
 |
justify why each step in the process of solving a linear equation is legal! |
JUSTIFICATION STRATEGY: The strategy is to solve the equation as we normally do,
but to include the reasons why what we did is "legal".
Be sure to show your solution steps.
Now is not the time to do the calculations in your head. |
Let' start with an easy example, so we can see what needs to be done.

Solve for x and justify each step with a reason: 5x + 4 = 29
|
Justification (Reasons): |
5x + 4 = 29 |
given equation |
5x + 4 - 4 = 29 - 4 |
Subtraction Property of Equality
subtract the same value from both sides of = sign |
5x = 25 |
Additive Inverse Property (left)
+ 4 - 4 = 0
Numerical Subtraction (right)
29 - 4 = 25
|
|
Multiplication Property of Equality
multiply both sides of = sign by the same value |
x = 5 |
Multiplicative Inverse Property (left)
5 • 1/5 = 1
Numerical Division (right)
25 ÷ 5 = 5 |
Yes, in the fourth step, you could have divided both sides by 5 and used "Division Property of Equality". The only drawback is that the needed "multiplicative inverse" reasoning in the fifth step would not be as "obvious" to someone reading your justification.
Some people may say that you would need to add a statement such as
"division by 5 is equivalent to multiplication by 1/5".
I know, picky, picky, picky. When in doublt, ask your teacher what is expected.

Let's now try something a little more challenging.
Solve for x and justify each step with a reason: 3(x - 2) + 5x = 9x - 24
|
Justification (Reasons): |
3(x - 2) + 5x = 9x - 24 |
given statement |
3x - 6 + 5x = 9x - 24 |
Remove the parentheses by the
Distributive Property
3(x - 2) = 3x - 6 |
3x + 5x - 6 = 9x - 24 |
Move the x's next to each other of the left side
Commutative Property of Addition
- 6 + 5x = + 5x - 6 |
8x - 6 = 9x - 24 |
Combine Like Terms
3x + 5x = 8x |
8x - 8x - 6 = 9x - 8x - 24 |
Subtraction Property of Equality
subtract the same value from both sides |
0 - 6 = x - 24 |
Additive Inverse Property (left)
8x - 8x = 0
Combine Like Terms (right)
9x - 8x = x |
-6 = x - 24 |
Additive Identity Property
0 - 6 = - 6 |
-6 + 24 = x - 24 + 24 |
Addition Property of Equality
add the same value to both sides |
18 = x + 0 |
Addition (left)
-6 + 24 = 18
Additive Inverse Property (right)
-24 + 24 = 0 |
18 = x |
Additive Identity Property
x + 0 = x |
The justification method shown above is an example of one method.
In this method, the expression "Combine Like Terms" was used.
"Combine Like Terms" can actually be broken down further using other
Real Number properties which will be shown in the next example.

Let's see how we can analyze "combine like terms".
This is a more intense breakdown of the properties involved.
 "Combining Like Terms" is broken down using reverse Distribuive Property, Addition, and Commutative Property. "Combining Like Terms" is broken down using reverse Distribuive Property, Addition, and Commutative Property.
Solve for x and justify each step with a reason: 4x - 1 + 5x = 12x - 22
|
Justification (Reasons): |
4x - 1 + 5x = 12x - 22 |
Given statement |
4x + 5x - 1 = 12x - 22 |
Commutative Property of Addition |
 x(4 + 5) x(4 + 5) - 1 = 12 x - 22 |
Distributive Property in reverse |
 x(9) x(9) - 1 = 12 x - 22 |
Numerical Addition |
 9x 9x - 1 = 12 x - 22 |
Commutative Property of Addition |
9x - 9x - 1 = 12x - 9x - 22 |
Subtraction Property of Equality |
x(9 - 9) - 1 = x(12 - 9) - 22 |
Distributive Property in reverse |
x(0) - 1 = x(3) - 22 |
Additive Inverse Property (left side)
9 - 9 = 0
Subtraction (right side)
12 - 9 = 3 |
0 - 1 = 3x - 22 |
Zero Property of Multiplication (left side)
x(0) = 0
Commutative Property of Multiplication (right)
x(3) =3x |
- 1 = 3x - 22 |
Additive Identity Property |
-1 + 22 = 3x - 24 + 22 |
Addition Property of Equality |
21 = 3x + 0 |
Numerical Addition (left side)
Additive Inverse Property (right side) |
21 = 3x |
Additive Identity Property |
| (1/3) • 21 = 3x • (1/3) |
Multiplicative Property of Equality |
| 7 = x |
Numerical Multiplication (left)
Multiplicative Inverse Property (right) |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|