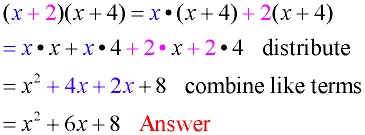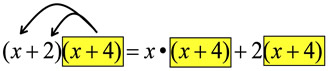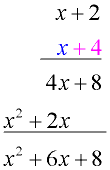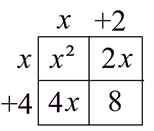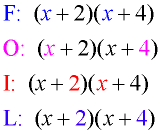|
When multiplying a binomial times a binomial, each term of the first binomial must be multiplied by each term of the second binomial.
Like terms are then combined.
|
(a + b)•(c + d) = ac + ad + bc + bd
Multiplying two binomials
When multiplying two binomials, four multiplications must take place. These multiplications can occur in any order, as long as each of the first two terms is multiplied by each of the second two terms.
There are numerous ways to set up the multiplication of two binomials. The two basic formats, horizontal line-up and vertical line-up, are similar to what we saw in adding and subtracting polynomials. Let's investigate the simple product (x + 2)(x + 4) with a variety of set-ups.
 Horizontal "Distributive" Set-up: (most commonly seen set-up) Horizontal "Distributive" Set-up: (most commonly seen set-up)
• Start with the first term of the first binomial (the blue x).
|
 |
• Distribute (multiply) this term times EACH of the terms in the second binomial (x + 4).
•
Then take the second term in the first binomial (including its sign: +2) and distribute (multiply) this term times EACH of the terms in the second binomial (x + 4).
• Add the results, combining like terms when needed.
• This method will work with all polynomials, not just binomials times binomials.
|
|
|
 Vertical "Distributive" Set-up: (same process as multiplication of numbers) Vertical "Distributive" Set-up: (same process as multiplication of numbers)
|
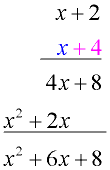 |
• Line up the binomials (or any polynomials) as you would for multiplying large numerical values.
•
Following the pattern of number multiplication, start with the right-hand term of the bottom binomial (+4). Multiply this value times both terms of the top binomial.
• Now move to the left-hand term of the bottom binomial (x). Multiply this value times both terms of the top binomial. Line up like terms as you write the answer.
• Add the columns. |
|
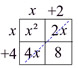
 "Grid" Set-up: (a table version of the distributive property clearly showing the 4 multiplications) "Grid" Set-up: (a table version of the distributive property clearly showing the 4 multiplications)
|
• Place one binomial at the top of the 2x2 grid (for binomials).
•
Place the other binomial on the left side of the grid.
• Position the terms so that each term (and its sign) lines up with a row or column of the grid.
• Multiply each intersecting row and column to fill the interior of the grid.
• Combine like terms in the interior of the grid.
Notice that the x-terms lie on the diagonal of the grid. |
|
The size of the grid can be adjusted to work with binomials, trinomials or other polynomials. |
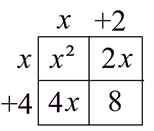
= x² + 2x + 4x + 8
= x² + 6x + 8 |
|

The next set-up works ONLY with binomials times binomials. While you may find this method helpful, you must remember that this method will not work in any other situations. For example, to multiply a binomial times a trinomial you will need to use one of the three more "universal" distributive methods stated above.
 "FOIL" Set-up: (for binomial multiplication ONLY!) "FOIL" Set-up: (for binomial multiplication ONLY!)
|
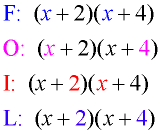
(x + 2)(x + 4)
= x² + 4x + 2x + 8
= x² + 6x + 8
|
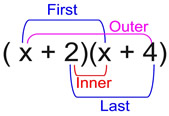
• Multiply First Outer Inner Last.
•
Add your results.
• Combine like terms.
• Remember that this method has limited usage (binomials only). |
|
This process is actually just a naming system for the distributive property as it relates to binomials (only). It creates the four needed multiplications. |
|
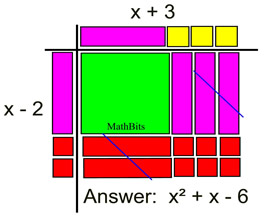
 Binomial Multiplication with Algebra Tiles: Binomial Multiplication with Algebra Tiles:
This set up of Algebra tiles gives you a "visual" demonstration of multiplying a binomial (x - 2) times a binomial (x + 3).
Key: 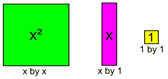
The red tiles represent negative values. The positive (purple) and negative (red) x-tiles cancel one another when reading the answer inside the grid. See more about Algebra Tiles. |
 |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|