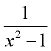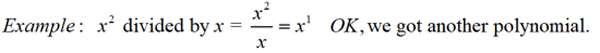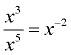|
 |
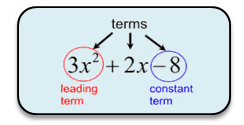
A polynomial is a finite sum of terms in which all variables have whole number exponents and no variable appears in a denominator. |
The leading term in a polynomial is the term of highest degree.
The constant term in a polynomial is the term without a variable.
Remember: NO negative exponents! NO fractional exponents!
Polynomials: YES or NO |
3x½ |
NO - exponent is not a whole number |
|
NO - the variable is in the denominator |
-3x2 |
YES - satisfies the polynomial definition |
|
NO - the square root of x can be written with a fractional exponent of x. |
2x-3 |
NO - exponent is not a whole number.
Negative exponent places x3 in denominator. |
|
YES - the exponent of x is 1 which is OK.
The coefficient being radical 3 is not a problem. |
|
|
Classification by Terms |
monomial |
one term: 12, 4x, x2, -5xy |
binomial |
two terms: 2x - 1, x2 - 4 |
trinomial |
three terms: x2 + 2x + 1 |
polynomial - one or more terms: polynomial means "many", but it can also be one term. |
The ending of these words "nomial"
is Greek for "part". |
Classification by Degree |
Linear - degree of 1 or 0: 3x + 1 or 12 |
Quadratic - degree of 2: 2x2 - x + 7 |
Cubic - degree of 3: 3x3 + 4x2 + 3x + 5 |
|
 |
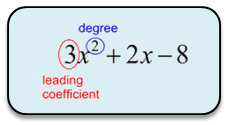
The degree of a polynomial is the highest degree of its terms.
Example: 3x2 + 4x + 1 has a degree of 2; x3 - x2 + 5x - 2 has a degree of 3
|
The standard form of a polynomial is when all like terms are combined and the exponents are arranged in descending order.
Polynomial: 2x + 3x5 + 4x3 - 8
Standard form: 3x5 + 4x3 + 2x - 8
3x5 + 0x4 + 4x3 + 0x2+ 2x1 - 8x0
"missing" terms have coefficient 0 |
|
Will we ever really use the degree?
Knowing the "degree" of a polynomial function will let you determine the most number of solutions the function may have,
and the most number of times the function may cross the x-axis. This is valuable information.
|
FYI: The standard form of a polynomial is formally written as anxn + an - 1xn - 1 + ... + a2x2 + a1x + a0,
where n is a non-negative integer, and a0, a1, a2, ..., an are real number constant coefficients with an ≠ 0.
|
 Polynomials and Closure: Polynomials and Closure:
Polynomials form a system similar to the system of integers, in that polynomials are closed under the operations of addition, subtraction, and multiplication.
CLOSURE: Polynomials will be closed under an operation if the operation produces another polynomial.
Adding polynomials creates another polynomial.
Subtracting polynomials creates another polynomial.
Multiplying polynomials creates another polynomial.
Dividing polynomials does not necessarily create another polynomial.
Polynomials are NOT closed under division (as you may get a variable in the denominator). |
• Closure under Addition: (2x2 + 3x + 4) + (x2 - 5x - 3) = 3x2 - 2x + 1
When adding polynomials, the variables and their exponents do not change. Only their coefficients will possibly change. This guarantees that the sum has variables and exponents which are already classified as belonging to polynomials. Polynomials are closed under addition.
• Closure under Subtraction: (2x2 + 3x + 4) - (x2 - 5x - 3) = x2 + 8x + 7
When subtracting polynomials, the variables and their exponents do not change. Only their coefficients will possibly change. This guarantees that the difference has variables and exponents which are already classified as belonging to polynomials. Polynomials are closed under subtraction.
• Closure under Multiplication: (x + 1)(x2 + 4x + 3) = x3 + 5x2 + 7x + 3
When multiplying polynomials, the variables' exponents are added, according to the rules of exponents. Remember that the exponents in polynomials are whole numbers. The whole numbers are closed under addition, which guarantees that the new exponents will be whole numbers. Consequently, polynomials are closed under multiplication.
What about division?
Polynomials are NOT closed under division. Yes, there are examples of division of polynomials that create polynomials:
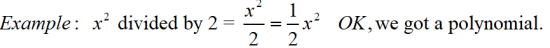
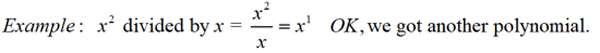
HOWEVER, look at this next simple counterexample, where a polynomial is NOT created.:
Example: 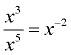 |
When dividing variables with exponents, there is the possibility of creating a negative exponent. Negative exponents are not allowed in polynomials.
(Also, a negative exponent on a variable places the variable in the denominator.)
|
|
(For more information about the similarities between the system of integers
and the system of polynomials, see Polynomials and Algebra Tiles.)

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|