|
Directions: Grab your paper and pencil. Write a solution to the following problems. Be sure to show your work to support your answer. Use your graphing calculator for checking only.
1. |
Consider the equation y = x2 - x - 6. Answer the following questions, stating how you arrived at your answer.
a) Determine whether the parabola opens upward or downward.
b) Find the y-intercept.
c) Find the x-intercepts, if any.
d) Find the equation of the axis of symmetry.
e) Sketch the graph. |
|
|
2. |
Given a quadratic function, which of the following choices explains the meaning of the zeros graphically.
|
|
|
3. |
Which of the following equations could describe the function seen in the graph at the right? (Check all that apply!) |
| |
|
|
|
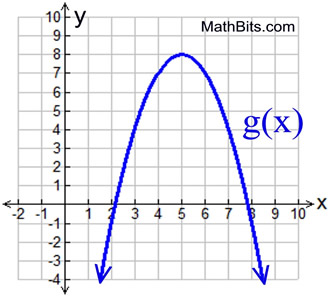
4. |
Shown below is the equation for function f (x), and the graph of parabolic function g (x). Which function has the larger maximum?
|
|
|
5. |
What is the equation of the axis of symmetry for this parabola? |
|
|
6. |
Which of the following statements is NOT true for the parabola seen in the graph? |
|
|
7. |
What is the equation of the axis of symmetry of the graph:
y =
3x2 + 6x - 1 |
|
|
8. |
Which equation could be the equation of the graphed parabola? |
|
|
9. |
What are the roots of the graphed parabola, assuming the roots to be integers? |
|
|
10. |
What is the vertex, or turning point, of the parabola y = 4x2 - 6x - 1?
|
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|