To MUTLIPLY rational expressions:
Factor first, reduce, and then multiply through.
Always reduce a factor from the top with a factor from the bottom! |
 Steps to Multiplying Rational Expressions:
Your teacher may, or may not, ask you to state the domains of rational expressions.
To multiply rational expressions, use the following "rule":
To multiply rational expressions:
1. Factor all numerators and denominators as much as possible.
2. Cancel (divide out) any common factors.
3. Multiply as shown in the rule above.
4. Check for any further simplifying of the answer.
The last step is not needed if step 2 was done correctly.
|
Examples:
Example 1:
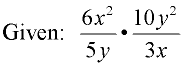
Domain: x ≠ 0; y ≠ 0
Multiply:
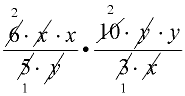
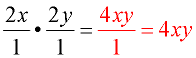
Domain: x ≠ 0; y ≠ 0
|
There is NO factoring to be done first in this example,
Reduce existing factors using your knowledge of the properties of exponents.
(Hint) If a problem involving exponents looks confusing, a listing of the individual factors may be helpful for seeing what can be reduced.
Multiply through the numerator.
Multiply through the denominator.
Check to see if the final answer can be reduced further, in case you did not reduce all factors prior to multiplying.
State the domain if directed by the problem or your teacher.
|
| |
Example 2:
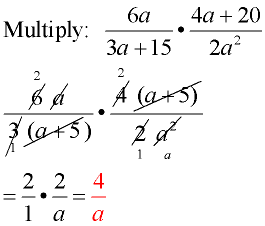
Domain: a ≠ 0, a ≠ -5
|
Factor first.
Reduce common factors.
 Do NOT reduce single terms from within parentheses containing a "+" or "-" sign. Reduce the entire parentheses.
State the domain if so directed by the problem or by your teacher. |
| |
Example 3:
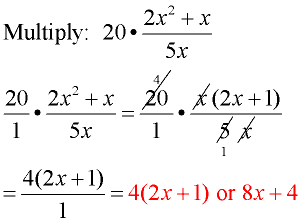Domain: x ≠ 0
|
Multiplying by 20 is the same as multiplying
by 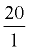 . Writing 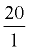may make the process more observable. Factor the numerator of the fraction.
Reduce common factors.
State the answer as directed by your teacher. |
| |
Example 4:
Multiply: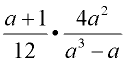 
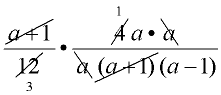
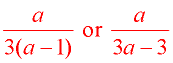
Domain: a ≠ -1, 0, 1
|
Factor first.
The denominator of the second fraction factors:
a3 - a = a(a2 - 1) = a(a + 1)(a - 1)
Reduce common factors (top with bottom).
Express your final answer in the form desired by your teacher, or by the form that may be stated in the problem (such as "in simplest form" or "in simplest factored form"). |
To DIVIDE rational expressions:
Flip second fraction, factor, reduce, multiply through.
Always reduce a factor from the top with a factor from the bottom! |
Steps to Dividing Rational Expressions:
Your teacher may, or may not, ask you to state the domains of rational expressions.
To divide rational expressions, use the following "rule":
To divide rational expressions:
1. Invert (flip) the second fraction (or bottom fraction).
2. Change the division sign to multiplication.
3. Follow the rules for multiplication |
Examples:
Example 1:
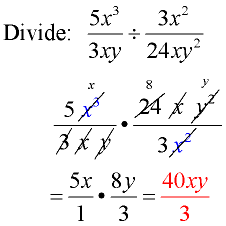
Domain: x ≠ 0, y ≠ 0 |
Flip second fraction and change division sign to multiply.
Factor.
Reduce common factors.
This example shows one way to reduce the factors.
Multiply.
State the domain if so directed by the problem or by your teacher. |
| |
Example 2:
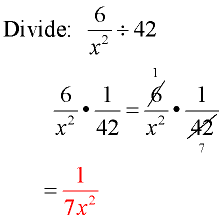Domain: x ≠ 0
|
Remember that 42 is really  .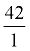
Flip second fraction and change to multiplication.
Factor and reduce common factors.
|
| |
|
Note the domain of the original problem:
Domain: x ≠ 0
Flip second fraction and change to multiplication.
Factor.
Reduce common factors.
Remember to reduce entire parentheses.
Multiply.
There is a problem with the domain in this example. When the "flip" occurred, the expression
"
x2 + 3x" became a denominator. Since 0 AND -3 make this flipped expression zero, we have an additional restriction (of x ≠ -3) to be placed on the domain. |
| |
Example 4:
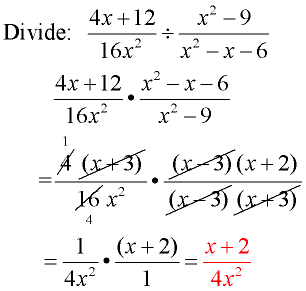Domain: x ≠ 0; x ≠ ± 3; x ≠ -2
|
Note the domain of the original problem:
Domain: x ≠ 0, x ≠- 2, x ≠3
Flip second fraction and change to multiplication.
Factor.
Reduce common factors.
Be careful to reduce entire parentheses.
When "x2 - 9" moved into the denominator, it added another restriction to the domain, x ≠ -3. |
|
