Systems of equations are also known as "simultaneous equations".
"Simultaneous" means being solved "at the same time".
When working with a "system" of equations, you are working with two or more equations at the same time. For our investigations, we will be working with two straight lines at a time (or two "linear equations" at a time).

Kyle's little sister, Jenny, claims that she can beat him in a snowmobile race to the next turn in the trail. Kyle takes the challenge and gives her a one minute head start. Jenny travels at 1640 feet per minute and Kyle travels at 2640 feet per minute. How long will it take Kyle to catch up with Jenny? |
 |
Solution:
Let d = distance in feet and t = time in minutes. (Remember distance = rate x time.)
Create TWO equations:
| |
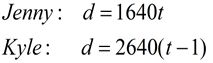 |
Kyle's time is one minute less than Jenny's time, since he gave her a head start. |
These equations can be graphed on a calculator. The graph shows that
Kyle catches Jenny after she has traveled for 2.64 minutes and he has traveled 4329.6 feet. Since Kyle left one minute behind Jenny, it took him 1.64 minutes to catch Jenny. |
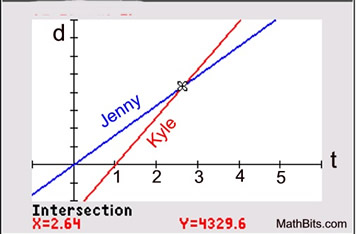 Y1 = 1640x and Y2 = 2640(x - 1)
Y1 = 1640x and Y2 = 2640(x - 1) |
The point where Jenny and Kyle meet (where the lines cross or intersect) is a point on the graph that makes both of the equations true.
 The solution to a system of equations is the point on a graph where the two equations intersect.
This is the point that makes both equations true. |

Solving Systems:
As the example above shows, the main task of working with linear systems is to find where the lines intersect (where they cross one another).
There are three main methods used for solving systems of linear equations. Two of them are algebraic techniques, and one is a graphical technique (as we saw in the example above).
• Substitution Method: The goal of this algebraic method is to replace one of the variables in one equation with an expression found by solving for that variable in the other equation.
• Elimination Method: The goal of this algebraic method is to eliminate one of the variables using addition or subtraction. The remaining equation will easily yield either the x or the y coordinate of the intersection point.
• Graphical Method: The goal of this graphical method is to solve the system by graphing the lines either on graph paper, or on the graphing calculator, and locating the point of intersection, in a manner similar to what was done with the example above.
When working with systems, remember that the equations of lines may appear in a variety of forms, such as: y = 2x + 1; -5x + y = 7; 4x + 2y = -5; y = 7
You may need to re-write the equations before beginning your solutions.
