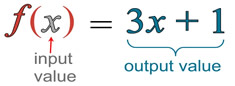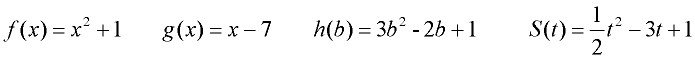|
We saw that a relation is simply a set of input and output values, represented in ordered pairs.
No special rules applied to a relation.
If we add a "specific rule" to a relation, we can get a function.
 The function "rule" is that a function has only one relationship for each x-value.
Remember, under the definition of a relation we saw that
an x-value could have more than one associated y-value.
Relation: {(1,1), (2,3),(5,5),(5,6)}
(The x = 5 has two possible y-values (both 5 and 6).)
This is not possible in a function.
|
A function is a set of ordered pairs in which each x-element has only ONE y-element associated with it.
|
|
|
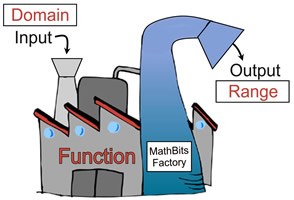
A function is like a factory machine that has input and output.
The input is the x-value
(called the "domain"),
and the output is the y-value
(called the "range")
of the function.
Each value "enters" the function only once, and has only "one value coming out" of the function.
|
While a function may NOT have two y-values assigned to the same x-value,
it may have
two x-values assigned to the same y-value.
NOT OK for a function:
{(5,1),(5,4)} |
OK for a function:
{(5,2),(4,2)} |
Function: each x-value has only ONE y-value!
|
|
Let's adjust our previous "relation" examples so they fit the function "definition".
The relationship between eye color and student names.
(x,y) = (eye color, student's name)
Relation: Set A = {(green, Steve), (blue, Elaine), (brown, Kyle), (green, Marsha), (blue, Miranda), (brown, Dylan)}
If we remove duplicate eye colors,
this eye color example
will be a function:
|
 |
Function: Set B =
{(blue, Steve), (green, Elaine), (brown, Kyle)}
|
Let's adjust this previous "relation" example so it fits the function "definition".
Relation:
(where x-values have
more than one y-value)
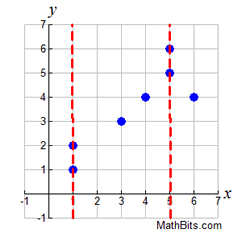
Relation:
{(1,1),(1,2),(3,3),(4,4),(5,5),(5,6),(6,4)}
|
Function:
If we remove (1,2) and (5,6),
we can create a function.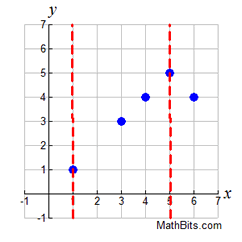
Relation:
{(1,1),(3,3),(4,4),(5,5),(6,4)}
|
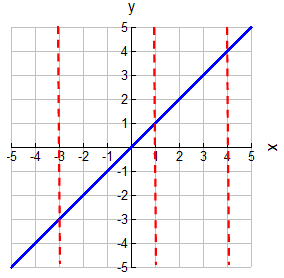
In this previous example, we saw that this straight line relation fits BOTH the definition of a relation and that of a function.
If vertical lines are drawn on this graph, the lines will only intersect the graph in ONE location, showing each x-value has only one y-value.
This relation was already a function.
|
|
Let's adjust this previous "relation" example so it fits the function "definition".
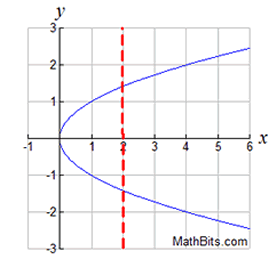
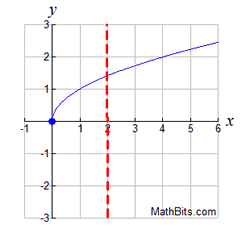
Notice that vertical lines on the graphs make it clear if an x-value had more than one y-value.
If the vertical lines intersected the graph in more than one location, we had a relation, NOT a function.
|
Vertical line test for functions: Any vertical line intersects the graph of a function in only ONE point. |
|
Given that relation A = {(4,3), (k,5), (7,-3), (3,2)}. Which of the following values for k will make relation A a function? Choices: a) 3 b) 4 c) 6
Solution: Choice c is the answer. The x-values of 3 and 4 are already used in relation A. If they are used again (with a different y-value), relation A will not be a function, as those x-values will be used more than once.
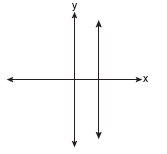
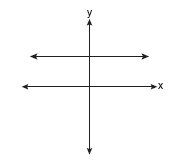
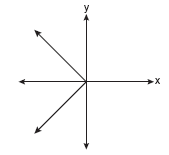
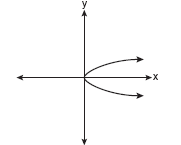
Which of the following graphs represents a function?
Solution: Choice b is the answer. A vertical line drawn on this graph will intersect the graph in only one location, making it a function. Vertical lines on the other three graphs will intersect the graph in more than one location, or as in part a, will intersect in an infinite number of points (all points).
|
Calculators graph functions! |
|
Most calculators (including the TI-84+ series) can only handle graphing functions.
The equation (function) must be in "y = " form before you can enter it in the calculator.
By solving for "y =", you are actually identifying a "function".
FYI: Function Notation:
While you will NOT be using function notation at this level,
you may be interested in knowing that it does exist. |
Function notation is the lettering style that is used to represent a function. The "y" value in the equation will be replaced with a different letter followed by a parentheses containing "x".
It is simply giving the function a fancier name.
For example, y = 3x + 2 would be written as f(x) = 3x + 2.
It is meant to be a precise way of giving information about the function without a rather lengthy written explanation.
For example: If two lines appear on the same graph, f(x) = 3x + 2 can clearly represent one of the lines and g(x) = 4x - 6 can clearly represent the other. Each function can have its own "name". There will be no confusion, such as might be possible with both equations reading "y =". (y = 3x + 2 and y = 4x - 6)
The most popular function notation is f (x) which is read "f of x".
This is NOT the multiplication of f times x.. |
|
|
Traditionally, functions are referred to by single letter names, such as f, g, h and so on.
Any letter(s), however, may be used to name a function.
Examples:
 
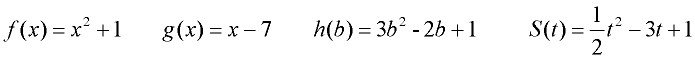
The f (x) notation is another way of representing the y-value in a function, y = f (x).
The y-axis may even be labeled as the f (x) axis, when graphing.
Ordered pairs may be written as (x, f (x)), instead of (x, y).
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
;
