Geometric Rules Quick Reference - MathBitsNotebook (Jr)

Geometric Rules Quick Reference
[Junior Level]
MathBitsNotebook.com

Topical Outline | JrMath Outline | MathBits' Teacher Resources

Terms of Use Contact Person: Donna Roberts

This is a partial listing of the more popular rules (theorems, postulates, and properties) that you will be using in your study of Geometry.

First a few words that refer to types of geometric "rules":

• A theorem is a statement (rule) that has been proven true using facts, operations and other rules that are known to be true. These are usually the "big" rules of geometry. A short theorem referring to a "lesser" rule is called a lemma.

• A corollary is a follow-up to an existing proven theorem. Corollaries are off-shoots of a theorem that require little or no further proof.

• A postulate (or axiom) is a statement (rule) that is taken to be true without proof. Euclid derived many of the rules for geometry starting with a series of definitions and only five postulates.

• A property is a quality or characteristic belonging to something.
For example, the real numbers have the associative, commutative and distributive properties.

Your textbook (and your teacher) may want you to remember these "rules" with slightly different wording.
Be sure to follow the directions from your teacher.

Angles:

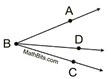
Adjacent Angles

Two angles that share a common vertex, a common side, and no common interior points (don't overlap).
m∠ABD and m∠DBC are adjacent. m∠ABC and m∠DBC are not adjacent

Linear Pair

Two adjacent angles whose non-common sides for a straight line.

Straight Angles

All straight angles are congruent (equal in measure).
(They all have a measure of 180º.)

Vertical Angles

Vertical angles are congruent (equal in measure).
m∠1 = m∠2
m∠3 = m∠4

Triangle Interior Sum

The sum of the measures of the interior angles of a triangle is 180º.

Exterior Angle

The measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles.

Angles forming a straight line

Angles around a point

Complementary Angles

Two angles the sum of whose measures is 90º.

Supplementary Angles

Two angles the sum of whose measures is 180º.

Triangles:

Pythagorean Theorem	c² = a² + b² In a right triangle, the square of the hypotenuse equals the sum of the square of the lengths of the legs.
Sum of Two Sides	The sum of the lengths of any two sides of a triangle must be greater than the third side.
Longest Side	In a triangle, the longest side is across from the largest angle.
Largest Angle	In a triangle, the largest angle is across from the longest side
Congruent Triangles	Triangles that are congruent if there corresponding angles are congruent and their corresponding sides are congruent.
Short-cuts to verify congruent triangles	SSS, ASA, AAS, SAS, HL(in right triangles)
Angle-Angle (AA) Similarity	If two angles of one triangle are congruent to two angles of another triangle, the triangles are similar.
Sides of Similar Δs	Corresponding sides of similar triangles are in proportion.

Parallels:

Corresponding Angles	If two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent.
Alternate Interior Angles	If two parallel lines are cut by a transversal, then the alternate interior angles are congruent.
Alternate Exterior Angles	If two parallel lines are cut by a transversal, then the alternate exterior angles are congruent.
Interiors on Same Side	If two parallel lines are cut by a transversal, the interior angles on the same side of the transversal are supplementary.

Quadrilaterals:

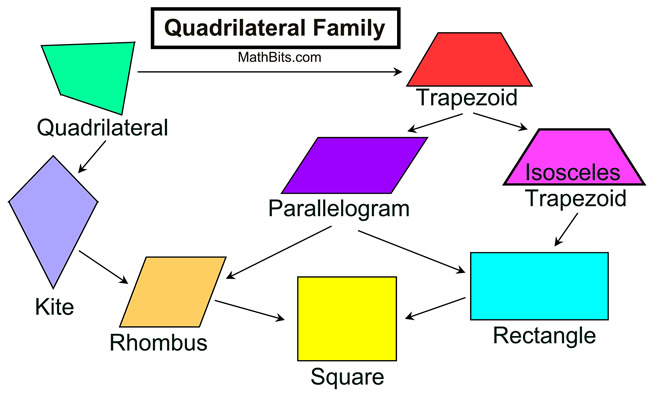
Quadrilateral	• is a four sided polygon • a figure with exactly four sides
Parallelograms	• is a quadrilateral w/ both pairs of opposite sides parallel • opposite sides are equal in length
Rectangle	• is a parallelogram with 4 right angles • two pairs of parallel sides • opposite sides of equal length
Rhombus	• is a parallelogram with all 4 sides of equal length • two pairs of parallel sides
Square	• is a parallelogram with 4 sides of equal length and 4 right angles • two pairs of parallel sides
Trapezoid	• quadrilateral with at least one pair of parallel sides
Isosceles Trapezoid	• is a trapezoid with congruent base angles • at least one pair of parallel sides • legs congruent
Kite	• is a quadrilateral with two sets of adjacent sides equal • not a trapezoid and not a parallelogram

Area (A), Volume (V), Surface Area (SA):

Rectangle	A_rectangle = l × w = b • h l= length; w = width; b = base; h = height
Parallelogram	A_{parallelogram} = b • h
Triangle	A_Δ = ½ • b• h
Trapezoid	A_trapezoid = ½ h (b₁ + b₂) or decompose
Regular Polygon	A_{regular polygon} = ½ • a • p a = apothem; p = perimeter
Circle (circumference)	C = 2πr = πd r = radius; d = diameter
Circle (area)	A_circle = πr²
Rectangular Solid (also called right rectangular prism)	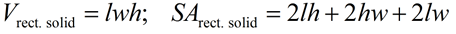SA formula assumes a "closed box" with all 6 sides.
Cube [special case of rectangular solid with all edges equal)	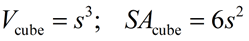SA formula assumes a "closed box" with all 6 sides. s = side
Cylinder	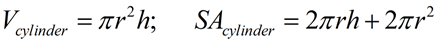SA formula assumes a "closed container" with a top and a bottom.
Cone	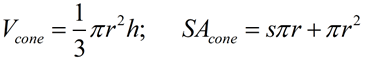SA formula assumes a "closed container", with a bottom. s = slant height
Sphere
Right Prism (rectangular or triangular)	V_{right prism} = B • h; SA = 2B + p • h B = area of the base; h = height; p = perimeter of base
Pyramid [assuming all of the faces (not the base) are the same]	B = area of the base; h = height; p = perimeter of base; s = slant height

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use".

Topical Outline | JrMath Outline | MathBitsNotebook.com | MathBits' Teacher Resources
Terms of Use Contact Person: Donna Roberts