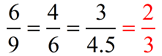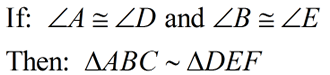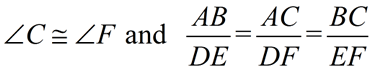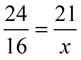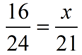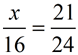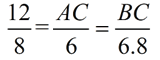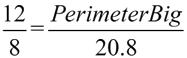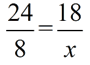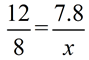|
Figures with the same shape, but not necessarily the same size,
are said to be "similar".
These cartoon dogs are exactly the same shape, but are not the same size.
The dog on the right is an enlargement
of the dog on the left.
While these dog figures are not congruent, they are similar. |
 |
|
 |
Polygons are similar if their corresponding angles are congruent (equal in measure) and the ratios of their corresponding sides are proportional. |
(This definition allows for congruent figures to also be "similar", where the ratio of the corresponding sides is 1:1.) |
Facts about similar triangles: |
 |
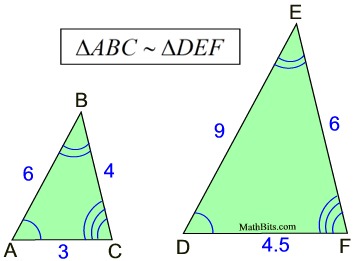
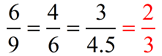
The ratio of the corresponding sides is called
the ratio of similitude or scale factor.
|
Similar Symbol:
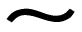 |
The symbol used to express "similar" was also seen in the symbol for "congruent" (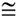 ). But unlike congruent, similar does not imply = size. ). But unlike congruent, similar does not imply = size. |
|
Similar figures are figures that are the same shape, but not necessarily the same size.
We saw, when working with congruent triangles, that it was not necessary to show all six characteristics of congruent triangles to verify that the triangles were actually congruent.
A similar idea applies to similar triangles.
AA |
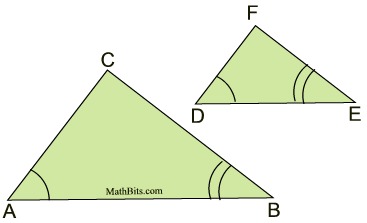
To verify two triangles are similar, it is sufficient to show that two angles of one triangle are congruent to the two corresponding angles of the other triangle. |
|
When dealing with 2 triangles, if you know that two sets of their angles are equal in measure, then the last pair MUST be equal, since the measures of the angles in all triangles add to 180º. So finding only 2 sets is sufficient.
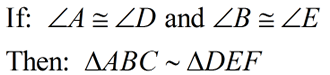
|
|
|
If two angles of one triangle are congruent to the corresponding angles of another triangle, the triangles are similar. |
There are additional methods for verifying similar triangles, but our investigation will be limited to this one method at this level.
Once the triangles are similar ...
the remaining set of angles will be congruent and the remaining corresponding sides will be in proportion.
|
The corresponding sides of similar triangles are in proportion. |

Measurements in Similar Figures: |
 Ratio of Lengths: Ratio of Lengths: |
|
Perimeters, Altitudes, Medians, Diagonals, Angle Bisectors |
If two polygons are similar, their corresponding sides, altitudes, medians, diagonals, angle bisectors and perimeters are all in the same ratio.
(Note that these are all "length" measurements.)
In similar figures, if the ratio of any of these corresponding lengths is expressed as 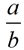 , ,
then the ratio of the other corresponding lengths can also be expressed as 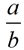 . .
|
Example: If the corresponding sides of two similar triangles are in the ratio 2:5, what is the ratio of their perimeters?
Answer: 2:5

 Ratio of Areas: Ratio of Areas: |
|
(square units) |
If two polygons are similar, the ratio of their areas is equal to the square of the ratio of their corresponding sides.
(Note that area is not a "length" measurement - it is a surface "area" measurement.)
In similar figures, if the ratio of two corresponding sides (or other lengths) is expressed as 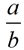 , ,
then the ratio of the ares can be expressed as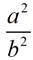 . .
|
|
Example:If the corresponding sides of two similar triangles are in the ratio 3:7, what is the ratio of their areas?
Answer: 9:49

 Ratio of Volumes: Ratio of Volumes: |
|
(cubic units) |
If two solids are similar, the ratio of their volumes is equal to the cube of the ratio of their corresponding sides.
(Note that volume is not a "length" measurement - it is a 3-D measurement.)
In similar figures, if the ratio of two corresponding sides (or other lengths) is expressed as 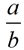 , ,
then the ratio of the volumes can be expressed as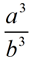 . .
|
|
Example: If the sides of two cubes are in the ratio 2:3, what is the ratio of their volumes?
Answer: 8:27

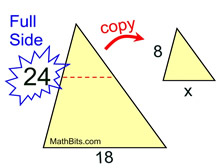
1. Find x.
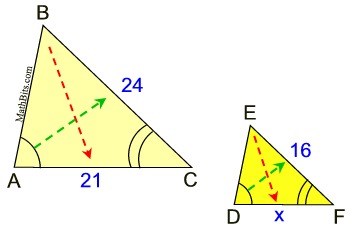 |
Solution:
The marked diagrams tell you the triangles are similar (AA is marked with arcs). The triangles seen in this problem are positioned such that their corresponding parts are in the same positions in each triangle. If the triangles are not positioned in this manner, match the corresponding sides by looking across from the angles. In this problem, 21 and x are across from the unmarked angles, and 24 and 16 are across from the angles marked with one arc. |
Create a proportion of the corresponding sides to solve for x. There are several options for setting up the proportion. The key is to be consistent in the set-up, and be sure the corresponding parts are in the same place in each fraction.
|

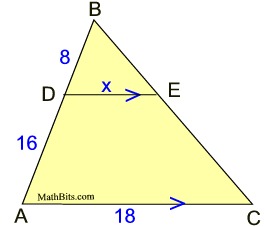
2. Find the perimeter of the larger triangle.
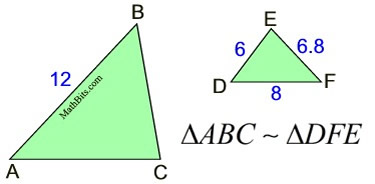 |
Solution:
Since the diagrams are not marked, match up the congruent angles by the letters in the names of the triangles. Vertex A matches with vertex D.
Vertex B matches with vertex F.
Vertex C matches with vertex E. |
Always read carefully to see WHAT you are supposed to find. This question asks you to find BE, which is a length of a side of a triangle.
Solution 1: Finding all sides of big triangle.
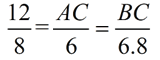
AC = 9
BC = 10.2
Perimeter big triangle = 31.2
|
Solution 2: Compare perimeters.
Perimeter of small triangle = 20.8.
Side ratio = 12 to 8 (large to small)
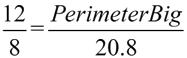 Perimeter big triangle = 31.2
Perimeter big triangle = 31.2
|
|


4. These rectangles are similar.
Find the value of x to the
nearest tenth of a unit.
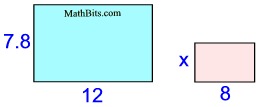 |
Solution:
Comparing length with length and width with width:
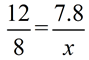
12 x = 62.4
x = 5.2 |
|
When you get to a high school Geometry course, you will learn more ways to deal with similar triangle problems.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|