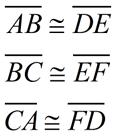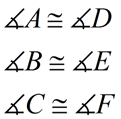|
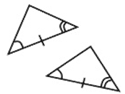
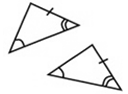
When triangles are congruent (identical), one triangle can be moved (through one, or more, rigid motions) to coincide with the other triangle. All corresponding sides and corresponding angles will be congruent.
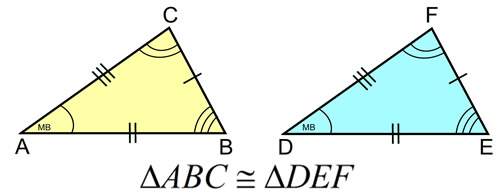
When triangles are congruent, six facts are always true.
|
Corresponding sides are congruent. |
Corresponding angles are congruent. |
|
|
The good news is that when trying to verify that two triangles congruent , it is not necessary to show that all six of these facts to be true. There are certain ordered combinations of these facts that are sufficient to verify triangles to be congruent. These combinations guarantee that, given these facts, it will be possible to draw triangles which will take on only one shape (be unique), thus insuring congruency.
Methods that Verify (Prove) Triangles Congruent |
The following ordered combinations of the congruent triangle facts
will be sufficient to verify (prove) triangles congruent (identical).
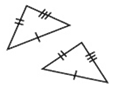
If three sides of a triangle are congruent to three sides of another triangle, the triangles are congruent. |
If two sides and the included angle of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent. |
If two angles and the included side of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent.
|
AAS (or SAA)
Angle-Angle-Side |
|
|
If two angles and the non-included side of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent.
This is an extension of ASA. In ASA, since you know two sets of angles are congruent, you automatically know the third sets are also congruent since there are 180º in each triangle.
|
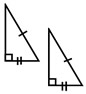
If the hypotenuse and leg of one right triangle are congruent to the corresponding parts of another right triangle, the right triangles are congruent. |
The "included angle" in SAS is the angle formed by the two sides of the triangle being used.
The "included side" in ASA is the side between the angles being used. It is the side where the rays of the angles overlap.
The "non-included" side in AAS can be either of the two sides that are not directly between the two angles being used. |
|
Once triangles are proven (verified) congruent, the corresponding leftover "parts" that were not used in SSS, SAS, ASA, AAS and HL, are also congruent.
Corresponding Parts of Congruent Triangles are Congruent. (CPCTC)
|

Methods that DO NOT Prove Triangles Congruent |
The following ordered combinations of the congruent triangle facts will NOT be sufficient to prove triangles congruent.
Let's see why these combinations DO NOT work!
|
|
This method will NOT prove triangles congruent! |
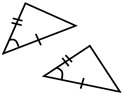
The AAA combination will show that the triangles are the same SHAPE (similar), but will NOT show that the triangles are the same size.
Example: Consider these two equilateral triangles that satisfy the AAA combination. They are the same shape, but are not the same size. Thus, they are not congruent. (They are similar.) |
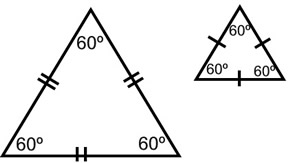 |
Yes, it is possible that the sides "could" be the same length and the triangles would be congruent, but this would be the exception, not the rule. |
|
SSA or ASS
Side-Side-Angle |
|
This method will NOT always prove triangles congruent! |
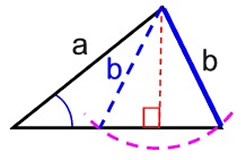
The SSA (or ASS) combination deals with two sides and the non-included angle. This combination is humorously referred to as the "Donkey Theorem". SSA (or ASS) is NOT a universal method to prove triangles congruent since it cannot guarantee that the shapes of the triangles formed will always be the same.
|
|
The problem with SSA (or ASS), is that the lengths of the sides being used, and their position in relation to the angle, do not always establish congruent triangles. Since the angle is not between the sides, side b, as shown below, is free to "swing" into one of two different positions. Two different triangles can be formed.
|
Since this method allows for the possibility of creating triangles of various shapes (and even no triangles at all in some cases), this method is not an accepted method to prove triangles congruent. |
For a more detailed explanation of the possible shapes issue, see http://mathbitsnotebook.com/Geometry/CongruentTriangles/CTtriangleMethods.html
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|