|
Mathematics is a form of a language. And as such, it has its own manner of communicating information. As you progress in your mathematical career, you will discover that mathematics relies more and more on its own set of symbols when discussing information.
Let's take a look at some of the geometry symbols we will be using.
(For information on the correct notation, using these symbols, see Notation.)
|
Geometric Symbol |
Interpretation |
Example |
|
Angle |
|
|
Triangle |
|
capital letter |
Point |
point A |
↔ |
Line |
|
|
Line Segment |
|
→ or ← |
Ray |
|
|| |
Parallel |
|
⊥ |
Perpendicular |
|
|
Congruent |
|
|
Similar |
|

Now, let's take a look at how figures are labeled in geometry, and the meanings of these labels. |
 |
Angles:
Lines:

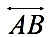 Lines are traditionally labeled by expressing two points through which the line passes.
Lines are traditionally labeled by expressing two points through which the line passes.
|
 line
line 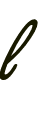 Lines may also be labeled with a single scripted letter, and referred to by that name.
Lines may also be labeled with a single scripted letter, and referred to by that name. |
Closed Figures:
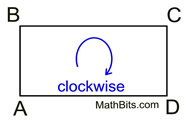 When drawing rectangle ABCD:
When drawing rectangle ABCD:
the letters must follow, in order, around the outside of the figure. You may start at any vertex point.
|
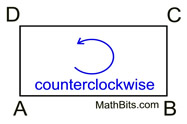 When drawing rectangle ABCD:
When drawing rectangle ABCD:
you may label in either a clockwise or counterclockwise direction around the outside of the figure. |
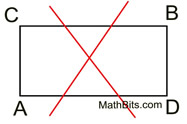 When drawing rectangle ABCD:
When drawing rectangle ABCD:
you may NOT label "across" the figure as shown here.
This is not rectangle ABCD.
(It is rectangle ACBD.) |
Triangles:
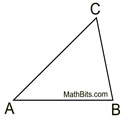  or any other three letter combination of A, B and C will apply to this triangle.
or any other three letter combination of A, B and C will apply to this triangle. |
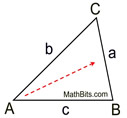 When using letters to refer to the sides of a triangle, it is customary to label the sides as small case letters. Across from the vertex labeled capital A will be the side labeled small case a, and so on.
When using letters to refer to the sides of a triangle, it is customary to label the sides as small case letters. Across from the vertex labeled capital A will be the side labeled small case a, and so on. |
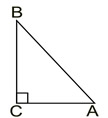 A right triangle is designated with a "box" drawn in the location of the right angle.
A right triangle is designated with a "box" drawn in the location of the right angle. |
Parallels and Perpendiculars:
Congruent Sides and Angles:
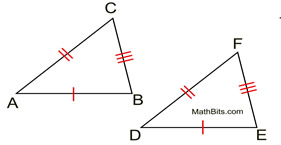  "Hash marks" are used to represent segments of equal length on diagrams. Notice that corresponding sides are distinguished by their number of hash marks. It is customary, with congruent triangles, to "letter" the triangles' names in a corresponding order: vertex A will correspond to vertex D, vertex B to vertex E, and vertex C to vertex F, so triangle ABC is congruent to triangle DEF.
"Hash marks" are used to represent segments of equal length on diagrams. Notice that corresponding sides are distinguished by their number of hash marks. It is customary, with congruent triangles, to "letter" the triangles' names in a corresponding order: vertex A will correspond to vertex D, vertex B to vertex E, and vertex C to vertex F, so triangle ABC is congruent to triangle DEF. |
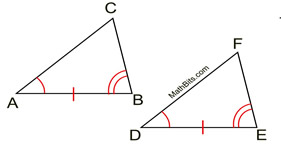
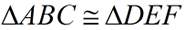
While
"hash marks" are used to represent segments of equal length on diagrams, "arcs" are used to represent angles of equal measure. In the same fashion as we saw with the hash marks, corresponding angles are distinguished by their number of arcs. |


NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|