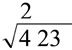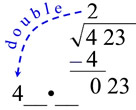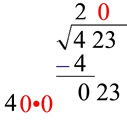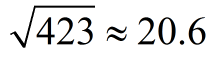|
The work on this page will be without a calculator.
Things to know before estimating: |
1. "Estimating" (or "approximating") a square root is not the same as "simplifying" a square root. Estimating (approximating) a square root changes the square root into a decimal form that is "close" to the square root's actual value. Whereas the process of simplifying a square root means finding another expression with the same value. "Simplifying" will be covered in the lesson on Simplifying Radicals.
2. The square roots of numbers that are not a perfect square are irrational numbers. These square roots cannot be expressed as a fraction. They will be non-repeating, non-ending decimal values. So, when estimating a square root, you are estimating a non-ending decimal. Remember that the square roots of perfect squares are known integers, There is no need to estimate these square roots.

 Estimating Square Roots without a Calculator Estimating Square Roots without a Calculator
The first step in estimating a square root is to get an idea of the size of the square root by comparing it to the square roots of two perfect squares.
For example: Compare 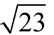 to the square roots of two perfect squares. to the square roots of two perfect squares.
 |
The number 23 falls between the perfect squares of 16 and 25.
Therefore 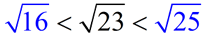 and
and 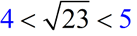 So, we know the square root of 23 is
So, we know the square root of 23 is
somewhere between 4 and 5,
and is closer to 5, since 23 is closer to 25, than it is to 16. |
|
While this "sandwich" idea of surrounding a square root with the square roots of perfect squares gives us a good idea of an approximate size of the square root, it does not give us any additional decimal information about the answer.
Getting a More Exact Estimate: |
 Method 1: Estimating Square Roots (Guess & Check Method) Method 1: Estimating Square Roots (Guess & Check Method)
As was done above, we are going to squeeze the square root between the square roots of two perfect squares. Then we will narrow in on more information about the answer.
Example: Estimate 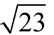 to the nearest tenth. to the nearest tenth.
Remember that we are looking for a number, when squared, that will be approximately 23.
| 1. Between which two perfect squares does 23 fall? |
1. 23 falls between 16 and 25
16 < 23 < 25 |
2. Establish as square roots.
|
2. 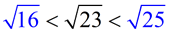 |
3. 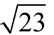 falls between 4 and 5. falls between 4 and 5.
|
3. 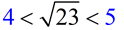 |
4. Let's guess at 4.5 and see where we stand.
Notice: 23 is closer to 25 than to 16, so the answer will be closer to 5. |
4. 4.52 = 20.25 (too small) |
| 5. Let's try 4.7. |
5. 4.72 = 22.09 (bit too small) |
| 6. Let's try 4.8. |
6. 4.82 = 23.04 (bit too large but really, really close) |
OK. So the value of 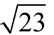 is somewhere between 4.7 and 4.8. is somewhere between 4.7 and 4.8. |
7. Let's check the hundredths place digit by trying 4.75.
This will tell us whether the rounded answer to the nearest tenth is 4.7 or 4.8. A more accurate answer will be a slight bit bigger than 4.75, but 4.75 shows us to round our answer up to 4.8. So, stop. |
7. 4.752 = 22.5625 |
| 8. When rounded to the nearest tenth, we now know our answer will round to 4.8. |
8. 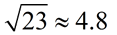 ANSWER ANSWER |
The "Guess and Check" method shown above is the easiest method to remember.
Simply "squeeze" the square root between the square roots of perfect squares,
then start guessing about what additional changes need to be made.

 Method 2: Estimating Square Roots (Averaging Method) Method 2: Estimating Square Roots (Averaging Method)
As was done above, we are going to squeeze the square root between the square roots of two perfect squares. Then we will narrow in on more information about the answer.
Example: Estimate 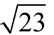 to the nearest hundredth. to the nearest hundredth.
Notice that we are going to the nearest hundredth this time.
| 1. Between which two perfect squares does 23 fall? |
1. 23 falls between 16 and 25
16 < 23 < 25 |
2. Establish as square roots.
|
2. 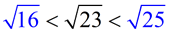 |
3. 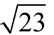 falls between 4 and 5. falls between 4 and 5.
|
3. 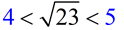 |
4. Divide 23 by either one of the perfect square roots.
(answers from here on can be rounded to 3 decimals) |
4. 23/4 = 5.75 |
| 5. Average 5.75 and 4. |
5. (5.75 + 4)/2 = 4.875 |
6. Repeat this process:
Now, divide 23 by 4.875. |
6. 23/4.875 = 4.718 |
| 7. Average 4.718 and 4.875 |
7. (4.718 + 4.875)/2= 4.797 |
You can start testing the answer as you go to see if you are close enough to 23.
Is 4.797 squared close enough to 23? The answer 23.011 is close enough. |
To the nearest hundredth the answer is 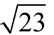 = 4.80 = 4.80 |
This method has a definite pattern that needs to be followed,
making this method harder to remember. The computations in
this method are more intense for working by hand.
It should be noted that the calculator lists
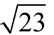 = 4.795831523 = 4.795831523

Optional Topic (not tested):
This topic is for your information only. It is not a topic that is usually tested in junior or senior high school. |
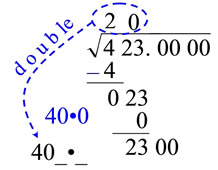
 Square Root Algorithm is a method for estimating squares roots that was taught prior to the use of calculators. Square Root Algorithm is a method for estimating squares roots that was taught prior to the use of calculators.
Example: Find 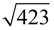 to the nearest tenth. to the nearest tenth.
Step 1: Group the numbers under the square root sign into pairs from right to left. It is not a problem if there is only one number left in the leftmost position (which will be 4 in this example). Each pair of numbers will yield one digit of the square root.
|
Step 2: Find the number whose square is less than or equal to the first pair (or first number) and write it above the square root line (which will be 2 in this example) .
|
|
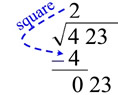
Step 3: Square this number, write it below the first digit (or pair), and subtract. Bring down the next pair of digits. |
|
Step 4: Double the number above the square root symbol line, and write it next to the problem as shown. Leave 2 empty spaces, separated with a multiplication dot, next to this number.
|
|
Step 5: Find a number, n, for the blank such that 4n x n will be less than or equal to 023. (4n means a two digit number where n is the ones digit. In this case it does not mean multiplication of 4 times n.)
41 x 1 = 41 which is > 23 40 x 0 = 0 which is < 23
Choose "0".
Put 0 on the top of the square root symbol.
|
|
Step 6: Multiply 0 times 40 and subtract from 23.
Step 7: Add a decimal point and pairs of zeros to 423.
Now repeat the steps 4 and 5.
Double the number above the square root, which will be 40, and write it next to the problem as shown. Leave 2 empty spaces, separated with a multiplication dot, next to this number.
|
|
Step 8: Find the number n, for the blank, such that 40n x n will be less than or equal to 2300.
405 x 5 =2025 Choose 5 for n.
Place 5 in the answer above the square root symbol (along with the decimal). Multiply 5 times 405 and subtract that amount (2025) from 2300.
Bring down the next pair of zeros. |
|
Step 9: And the process continues in the same manner.
Double the number above the square root symbol. Leave 2 empty spaces, separated with a multiplication dot, next to this number.
Find the number n, for the blank, such that 410n x n will be less than or equal to 27500.
4106 x 6 =24636 Choose 6 for n. |
|
| Step 10: Place 6 in the answer above the square root symbol. Multiply 6 times 4106 and subtract that amount (24636) from 27500.
We will stop at this step, since we are rounding to the nearest tenth. If needed, we could keep going (repeating the same process) to obtain more decimal values.
ANSWER: 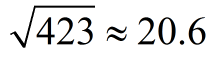 |
|
|