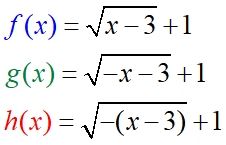|
The transformations you have seen in the past
can also be used to move and resize graphs of functions.

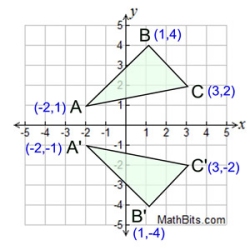
| Reflection: Over x-axis: - f (x) |
Think about what you know about reflections over the x-axis.
The graph at the right should look familiar.
During the reflection, what happened to the x-values?
The answer is "nothing, they stayed the same".
During a reflection in the x-axis, the x-values do not change.
During the reflection, what happened to the y-values?
The answer is "they changed their sign, they were negated".
During a reflection in the x-axis, the y-values are negated.
rx-axis (x, y) = (x, -y) |
|

Let's apply this information to functions reflected in the x-axis.
 When looking for a mirror image of a function When looking for a mirror image of a function
(a reflection) in the x-axis,
the x-values will remain the same,
and the y-values will be negated.
If g(x) is the reflection of f (x) in the x-axis, then
g(x) = - f (x)
g(x) = -1• f (x)
Any points that lie "on" the x-axis
will stay right where they are
(they will not move)
during a reflection in the x-axis.
|
Given: f (x) = 2x
the reflection in the x-axis will be:
-f (x) = -(2x)
The new reflection function can be renamed:
g (x) = -(2x)
|
 A reflection over the x-axis negates the y-values only. A reflection over the x-axis negates the y-values only.

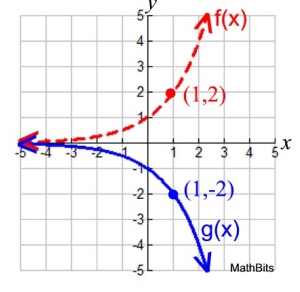
| Reflection: Over y-axis: f (-x) |
Think about what you know about reflections over the y-axis.
The graph at the right should look familiar.
During the reflection, what happened to the x-values?
The answer is "they changed their signs, they were negated".
During a reflection in the y-axis, the x-values are negated.
During the reflection, what happened to the y-values?
The answer is "nothing, they stayed the same".
During a reflection in the y-axis, the y-values do not change.
ry-axis (x, y) = (-x, y) |
|

Let's apply this information to functions reflected in the y-axis.
 When looking for a mirror image of a function When looking for a mirror image of a function
(a reflection) in the y-axis,
the y-values will remain the same,
and the x-values will be negated.
If g(x) is the reflection of f (x) in the y-axis,
then
g(x) = f (-x)
Any points that lie "on" the y-axis
will stay right where they are
(they will not move)
during a reflection in the y-axis.
 A reflection over the y-axis A reflection over the y-axis
negates the x-values only.
|
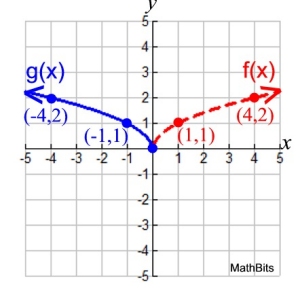
Given: 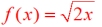
the reflection in the y-axis will be:
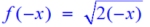
The new reflection function can be renamed:
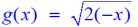
Notice how positive values of x cause
the square root to be undefined.
Only negative values (or zero) yield an answer.
|

A potential "tricky" spot when working with reflecting
transformed functions over the x-axis:
When applying the negative sign to signal a reflection of a transformed function,
be sure to negate the ENTIRE function that you wish to flip
(if you want the reflection in the x-axis). |
Compare the two situations shown below.
Which one is correct depends upon what you were trying to accomplish.
If the task was to flip the entire graph f (x) over the x-axis, the correct situation is on the right.
Remember, reflections in the x-axis are changing the y-values from the function.
 f (x) = | x | + 1 f (x) = | x | + 1
g(x) = -| x | + 1
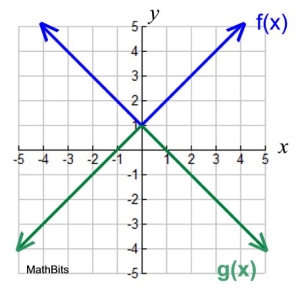
The reflection that occurred here was:
a reflection of the parent function,
y = | x |,
in the x-axis,
and then a vertical shift of 1 occured. |
 f (x) = | x | + 1 f (x) = | x | + 1
g(x) = -(| x | + 1)
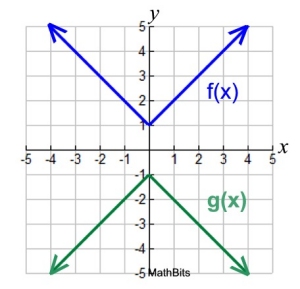
The reflection that occurred here was:
a reflection of the entire function f (x)
in the x-axis,
to obtain the graph shown above. |
What about reflecting over the y-axis?
A somewhat similar situation may pop up with
reflections over the y-axis,
where the reflection is focused on
negating the x-value (not the y-value).
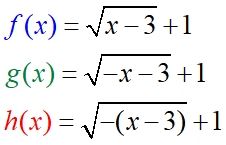
Note, negating only the x-value
gives a reflection over the y-axis. |
 |
In some cases, the nature of the equation may affect the use of a negative symbol, as seen with absolute value (also with squaring).
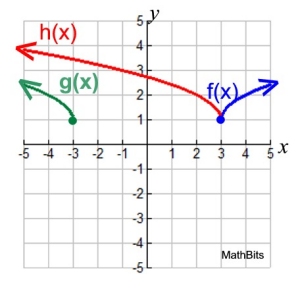
f (x) = | x - 3 | + 1
g(x) = | -x - 3 | + 1
reflection in the y-axis
h(x) = | -(x - 3) | + 1
h(x) is the same function as f (x)
due to the absolute value function at work. |
 |

S U M M A R Y
Reflections of Functions: -f (x) and f (-x) |
 Reflection over the x-axis. Reflection over the x-axis.
-f (x) reflects f (x) over the x-axis
|
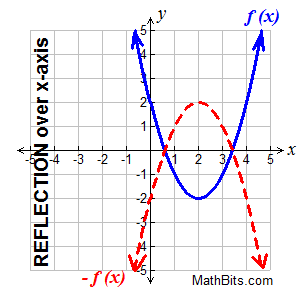 Reflections over the x-axis keep the Reflections over the x-axis keep the
x-values the same, and
negates the y-values. |
Vertical Reflection:
Reflections are mirror images. Think of "folding" the graph over the x-axis.
On a grid, you used the formula
(x,y) → (x,-y) for a reflection in the
x-axis, where the y-values were negated.
Keeping in mind that y = f (x),
we can write this formula as
(x, f (x)) → (x, -f (x)).
|
 |
|
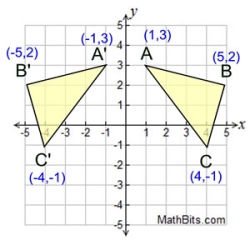
 Reflection over the y-axis.
f (-x) reflects f (x) over the y-axis Reflection over the y-axis.
f (-x) reflects f (x) over the y-axis |
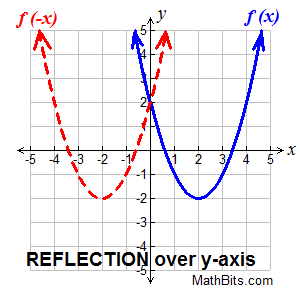 Reflections over the y-axis keep the Reflections over the y-axis keep the
y-values the same, and
negates
the x-values. |
Horizontal Reflection:
Reflections are mirror images. Think of "folding" the graph over the y-axis.
On a grid, you used the formula (x,y) → (-x,y) for a reflection in the y-axis, where the x-values were negated.
Keeping in mind that y = f (x),
we can write this formula as (x, f (x)) → (-x, f (-x)).

|
For information on the concept of reflecting over y = x, y = -x, or any line,
see Refresher: Reflections.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|