|
The transformations you have seen in the past
can also be used to move and resize graphs of functions.
| Translation: Horizontal Shift: f (x + k) |
 A function can be moved left (or right) by adding a constant to the x-value.
This movement is called a horizontal shift.
It is movement along the x-axis.
The constant value to be added is represented as "k".
Horizontal Shift: f (x + k)
• k > 0 slides to the left
|
| • k < 0 slides to the right |
| • k = 0 no movement |
|
When dealing with "k", the sign (±) indicates
the "direction" of the movement.
The actual distance traveled is always positive, | k |,
as distance and units of measurement are positive.
BE CAREFUL: When dealing with a
horizontal shift, the "direction" of k > 0 is left,
and the "direction" of k < 0 is right. |
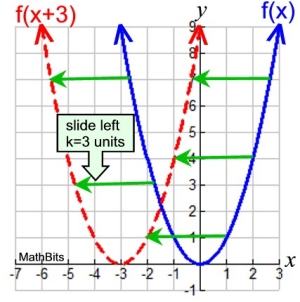
Given: f (x) = x2 and k = 3
A horizontal shift of 3 units will
move the graph 3 units to the left.
Horizontal Shift:
f (x+3) = (x+3)2
The new function can be renamed:
g (x) = ( x + 3 )2
|
Every point in a function graph will move directly
left (or right) in a horizontal shift.
(x, y) → (x + k, y)
 A horizontal shift deals with changing ONLY the x-values.
 |
Wait a minute!!
Shouldn't a positive "k" move to the right (not to the left)????
While this seems like a logical assumption, it is NOT true.
Let's look at the example below to see if we can figure out
why this logical assumption is NOT true. |
|
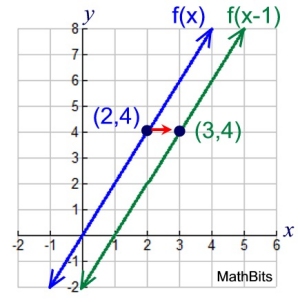
Consider the function f (x) = 2x and its translation f (x + 1) = 2(x + 1).
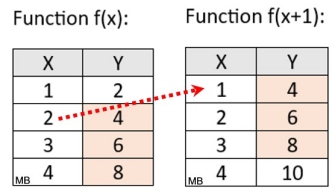
Let's concentrate on the y-values of 4, 6 and 8.
Notice, in f (x+!) how the
x-values associated with
these y-values of 4, 6, and 8
are
smaller values of x.
To maintain these
same y-values,
1 must be subtracted from
the x-values. The graph of f (x+1) is "backing up" from
function f (x).
It is moving to the left of f (x). |
 |
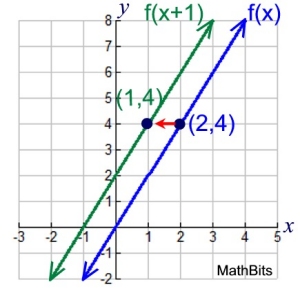The tables above show a glimpse of the relationship between the two functions.
Remember we are "translating" the function,
which means we want to slide it without changing its shape.
And since this is a horizontal "slide", we want the y-values to stay the same.
The tables show that if we use " x + 1" to replace " x",
we will need to
subtract 1 from the x-values
to maintain the same y-values.
Subtracting from the x-values means moving to the left.
So, when " k" is greater than zero, the translation is to the left (not the right).
Same type of analysis applies for f (x - 1).
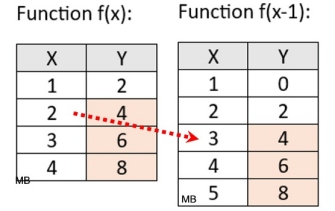
Notice, in f (x-!) how the
x-values associated with
the y-values 4, 6, and 8 are
larger values of x.
In order to maintain the
same y-values,
1 must be added
to the x-values.
The graph of f (x-1) is "ahead of" the function f (x).
It is moving to the right of f (x). |
|
The tables show that if we use "x - 1" to replace "x", we will need to add 1 to the x-values
to maintain the same y-values. Adding to the x-values means moving to the right.
So, when "k" is less than zero, the translation is to the right (not the left).
This whole concept hinges on what happens to the x-values
when you alter the y-values. |
a) Given  .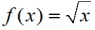
b) State the equation, g(x), that represents a horizontal shift of k = -3 to f (x).
c) Graph g(x). Describe how the graph of g(x) is formed.
d) The point (1,1) is located on f (x). What will be the coordinates of this point after the horizontal shift?
e) State the domain and range of f (x) and g(x). |
Solutions:
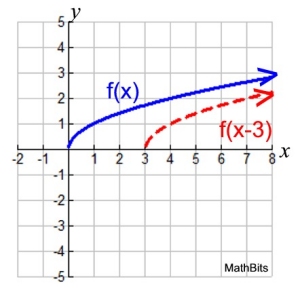
a) See graph
b) f (x) is the parent function for square root.
g(x) = f (x - 3)
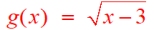
c) See graph.
Every point of f (x) slides directly "right" 3 units,
forming function g(x). The graph of g(x) is a horizontal
shift of
the function f (x).
d) The point will be (4, 1). The x-value was increased by 3 units.
Notice how (0,0) from f (x), becomes (3,0) for g(x).
e) Domain of f (x): [0,∞). Domain of g (x): [3,∞)
Range of f (x): [0,∞). Range of g (x): [0,∞) |
 |
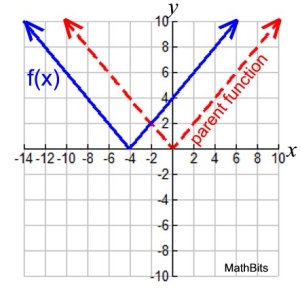
a) Graph f (x) = | x + 4 | using your knowledge of its parent function.
b) Describe the transformation that has occurred in this problem.
c) The turning point for the parent function is located at (0,0). What is the turning point of f (x)?
d) State the domain and range of the parent function and of f (x).
|
Solutions:
a) The parent function is the simplest absolute value function g(x) = | x |
(You need to remember the graph of the parent function of absolute value.)
b) The parent function, g(x), was transformed by a horizontal shift of 4 units to the left to produce the function f (x).
c) (-4,0)
d) Domain of f (x): (-∞,∞). Domain parent: (-∞,∞)
Range of f (x): [0,∞). Range parent: [0,∞) |
 |
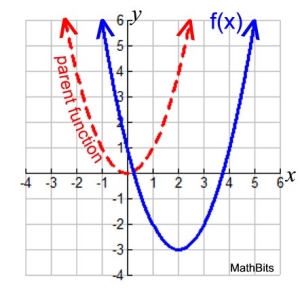
This example combines a vertical shift with a horizontal shift.
a) Graph the function f (x) = (x - 2)2 - 3.
b) What is the parent function associated with this transformation?
c) Describe the movement of this function from the parent function.
d) State the coordinates of the minimum points of the parent function and of f (x).
e) State the domain and range of the parent function and of f (x).
|
Solutions:
a) See the graph.
b) The parent function is a quadratic function, y = x2.
c) From the parent function, f (x) is shifted horizontally 2 units to the right. It is also shifted vertically 3 units down.
f (x) moves 2 to the right, and 3 down.
d) minimum point of parent:(0,0)
minimum point of f (x): (2,-3)
e) Domain of f (x): (-∞,∞). Domain parent: (-∞,∞)
Range of f (x): [-3,∞). Range parent: [0,∞) |
 |
S U M M A R Y
Translation of Functions: f (x + k) called a Horizontal Shift |
Translation horizontally (left or right)
f (x + k) translates f (x) left or right |
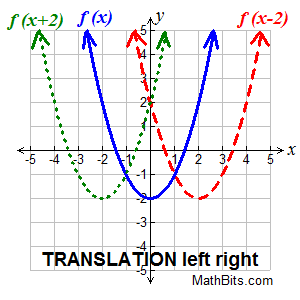
Changes occur "inside" the function
(affecting the x-axis). |
Horizontal Shift:
This translation is a "slide" left or right.
• if k > 0, the graph translates to the left k units.
• if k < 0, the graph translates to the right k units.
This one will not be obvious from the patterns you previously used when translating points.
k positive moves graph left
k negative moves graph right
A horizontal shift means that every point ( x,y) on the graph of f ( x) is transformed to ( x - k, y) or ( x + k, y) on the graphs of y = f ( x + k) or y = f ( x - k) respectively.
Look carefully as this can be very confusing!
|
Hint: To remember which way to move the graph, set (x + k) = 0. The solution will tell you in which direction to move and by how much.
f (x - 2): x - 2 = 0 gives x = +2, move right 2 units.
f (x + 3): x + 3 = 0 gives x = -3, move left 3 units. |
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
