Functions: Vertical Stretch or Compress MathBitsNotebook.com Topical Outline | Algebra 1 Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

When a function is multiplied by a positive constant, k,
a vertical stretch, or compression, of the function will occur.

If the constant is greater than one (k > 1), a vertical stretch will occur.
If the constant is between 0 and 1 (0 < k < 1), a vertical compression will occur.

FYI: If it appears that k is negative, you are looking at a vertical stretch, or compress,
followed by a vertical reflection (in the x-axis).
Remember: a reflection of f (x) in the x-axis is -f (x) or -1•f (x).
For example, -2(f (x)) = -1• 2(f (x)) where the reflection is more obvious.

A vertical stretch, or compress, will multiply all y-values by k. The x-values will not change. (x, y) → (x, k • y ) NOTE: During a vertical stretch, or compress, the root values of the function (where y = 0), never change. They stay attached to the x-axis.

A vertical stretch, or compression,
transforms the "outside" (output values) of the function.

Vertical Stretch:    k f (x) where k > 1 If the starting y-coordinate is positive, the vertical stretch will move the new y-coordinate further above the x-axis. If the starting y-coordinate is negative, the vertical stretch will move the new y-coordinate further below the x-axis. Remember: The root values (where y = 0) stay attached to the x-axis. They never change. A vertical shift "pulls" the graph vertically away from the x-axis (up or down). (It's like "pulling taffy".)

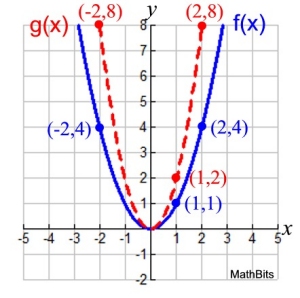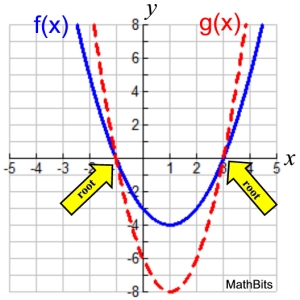
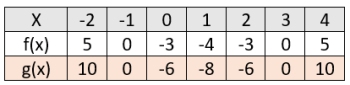
\ Given: f (x) = x2    and   k = 2 The outputs from this stretch will be twice the outputs from f (x). This is a scale factor of 2. 2 f (x) = 2(x2) The new function can be renamed: g (x) = 2 ( x2 )

Vertical stretch with k = 2 Given: f (x) = x2 - 2x - 3  and  k = 2 2 f (x) = 2(x2 - 2x - 3) Renamed:    g(x) = 2(x2 - 2x - 3) Notice that the graph is "pulled" away (stretched), both above and below the x-axis. The roots (at x = -1 and x = 3) do not change. The function and its vertical stretch will be equal at these points. f (x) = g(x) at x = -1 and x = 3

A vertical stretch will multiply ONLY the y-values.
(You are working "outside" the function, with the outputs.)

Vertical Compression:    k f (x) where 0 < k < 1 The difference between a vertical stretch and a vertical compress is the size of the number that is multiplied times the y-value. If you are multiplying by a number between zero and one, you are multiplying by a small fraction. If the starting y-coordinate is positive, the vertical compression will move the new y-coordinate above, but closer to, the x-axis. If the starting y-coordinate is negative, the vertical compression will move the new y-coordinate below, but closer to. the x-axis. A vertical compression "pushes" the graph vertically closer to the x-axis.

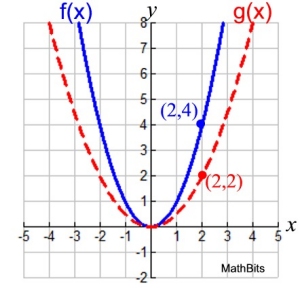
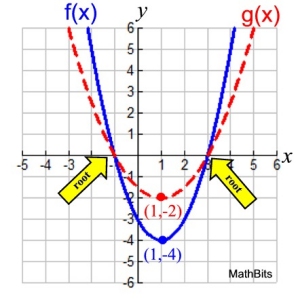
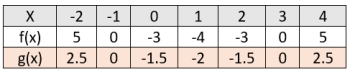
f (x) = x2    and  k = ½ The outputs from this stretch will be half the outputs from f (x). This is a scale factor of ½. ½ f (x) = ½ (x2) The new function can be renamed: g (x) = ½ ( x2 ) Root value (0,0) has no change.

In the example above, the inputs of the graphs were not changed.
During the transformation, the outputs of f (x) were multiplied by a factor of ½, (k = ½),
which compressed the graph f (x) vertically.

When working with quadratic functions, a vertical compression makes the parabola look wider
(the width across the parabola gets larger).

Vertical compression with k = ½ Given: f (x) = x2 - 2x - 3  and   k = ½      ½ f (x) = ½(x2 - 2x - 3) Renamed: g(x) = ½(x2 - 2x - 3) Notice that the graph is "pushed" (compressed) toward the x-axis, both above and below the x-axis. The roots (at x = -1 and x = 3) do not change. The function and its vertical compression will be equal at these points. f (x) = g(x) at x = -1 and x = 3

A vertical compression will multiply ONLY the y-values.
(You are working "outside" the function, with the outputs.)

S U M M A R Y

Dilations of Functions:     Vertical Stretch / Compress:    k • f (x)
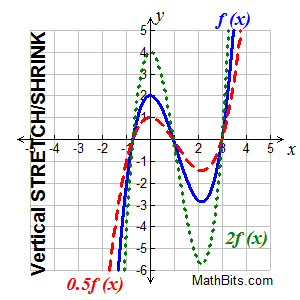
Vertical Stretch or Compression (Shrink)     k f (x) stretches/shrinks f (x) vertically	"Multiply y-coordinates": (x, y) becomes (x, ky) "vertical dilation"
A vertical stretching is the stretching of the graph away from the x-axis A vertical compression (or shrinking) is the squeezing of the graph toward the x-axis. • if k > 1, the graph of y = k•f (x) is the graph of f (x) vertically stretched by multiplying each of its y-coordinates by k. • if 0 < k < 1 (a fraction), the graph is f (x) vertically shrunk (or compressed) by multiplying each of its y-coordinates by k . • if k should be negative, the vertical stretch or shrink is followed by a reflection across the x-axis.
Notice that the "roots" on the graph stay in their same positions on the x-axis. The graph gets "taffy pulled" or "pushed" up and down from the locking root positions. The y-values change.