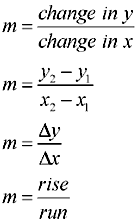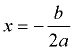|
 
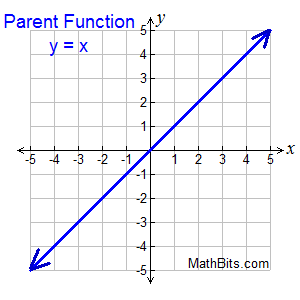
Unless otherwise stated:
Domain: 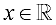 (All Reals) (All Reals)
Range: 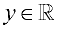 (All Reals) (All Reals)
|
Equation Forms:
• Slope-Intercept Form:
y = mx + b
m = slope; b = y-intercept
• Point-Slope Form:
y - y1 = m(x - x1)
uses point (x1,y1) and m
• Standard Form:
Ax + By = C
A, B and C are integers.
A is positive.
|
|
Finding Slope:
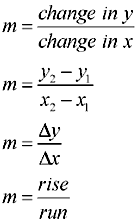
Average rate of change (slope) is constant. |
| No relative or absolute maxima or minima unless domain is altered. |
x-intercept (for y = x):
crosses x-axis
(x, 0)
Set y = 0, solve for x.
y-intercept (for y = x):
crosses y-axis
(0, y)
"b" value
Set x = 0, solve for y.
End Behavior:
One end approaches +∞,
other end approaches -∞.
(Unless domain is altered.)
|
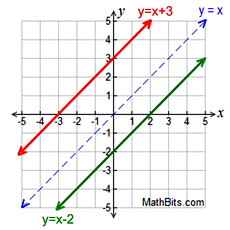
Effects of Changes in y = mx + b: (m = slope; b = y-intercept)
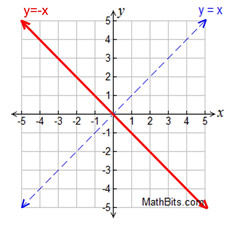
• if m = 0, then line is horizontal (y = b)
• if m = undefined, then line is vertical ("run" =0) (not a function)
• if m > 0, the slope is positive (line increases from left to right)
(the larger the slope the steeper the line)
• if m < 0, the slope is negative (line decreases from left to right)
• Lines with equal slopes are parallel.
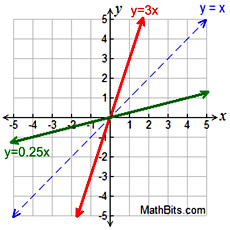
• | m | > 1 implies a vertical stretch
• -1 < m < 0 or 0 < m < 1, implies a vertical shrink
• if b > 0, then there is a vertical shift up "b" units
• if b < 0, then there is a vertical shift down "b" units |
|
Linear Function - Transformation Examples:

 |
Equation Forms:
• Vertex Form:
y = a(x - h)2 + k
with
vertex (h,k)
shows vertex, max/min, inc/dec
• Point-Slope Form:
y = ax2 + bx + c
negative "a" opens down
• Intercept Form:
y = a(x - p)(x - q)
p and q are x-intercepts.
shows roots, pos/neg
|
|
Axis of Symmetry:
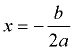 locates "turning point"
locates "turning point"
(vertex)
Average rate of change
NOT constant
x-intercept(s):
determine roots/zeros
y-intercept:
(0, y)
|
End Behavior: Both ends approach +∞,
or both ends approaches -∞.
Quadratic Function - Possible Real Roots:
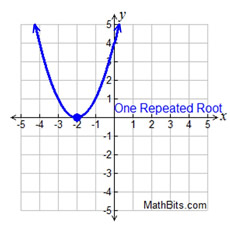 y = (x + 2)(x + 2)
y = (x + 2)(x + 2)
x = -2; x = -2 |
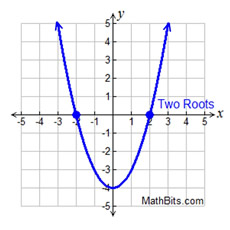 y = (x - 2)(x + 2)
y = (x - 2)(x + 2)
x = 2; x = -2 |
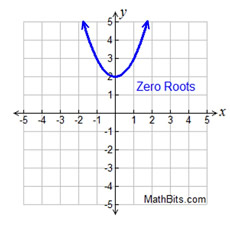 y = x
y = x² + 2
roots are complex (imaginary)
|
Maximum/Minimum: Finding the "turning point" (vertex) will locate the maximum or minimum point. The intervals of increasing/decreasing are also determined by the vertex.
Quadratic Function - Transformation Examples:
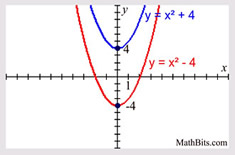
Translation
|
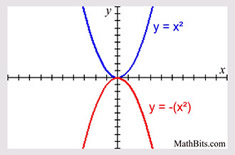
Reflection
|
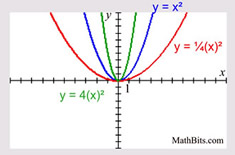
Vertical Stretch/Shrink |

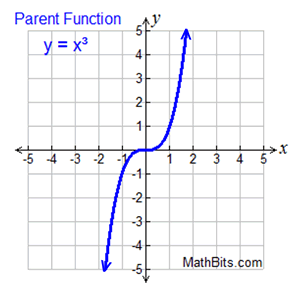 Cubic functions are of degree 3.
Cubic functions are of degree 3. |
Example Equation Forms:
• y = x3
(1 real root - repeated)
• y = x3- 3x2= x2(x - 3)
(two real roots - 1 repeated)
• y = x3+2x2+x = x(x + 1)2
(three visible terms)
• y = x3+3x2+3x+1=(x+1)3
(1 real root - repeated)
• y = (x+1)(x - 2)(x - 3)
(factored form - 3 real roots)
|
|
Symmetric (for y = x³):
about origin
Average rate of change:
NOT constant
x-intercept(s):
determine roots/zeros
y-intercept:
(0, y)
End Behavior:
One end approaches +∞,
other end approaches -∞.
(Unless domain is altered.)
|
Cubic Function - Possible Real Roots:
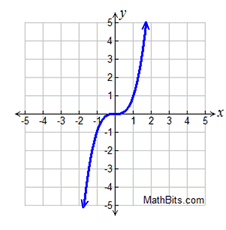 y = x³
y = x³
1 Real Root (repeated) |
 y = x³ - 3x²
y = x³ - 3x²
2 Real roots (1 repeated) |
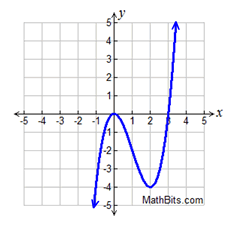
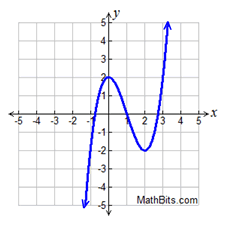 y = x
y = x³ - 3 x² + 2
3 Real roots |
Cubic Function - Transformation Examples:
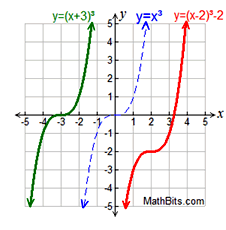
Translations |
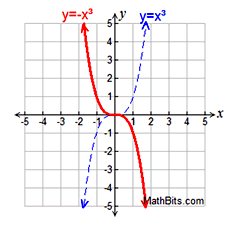 Reflection
Reflection |
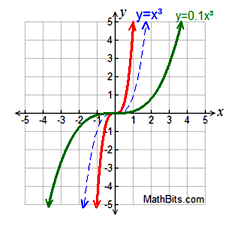
Vertical Stretch/Shrink |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|