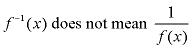|
 |
The inverse of a function is the set of ordered pairs obtained by interchanging the first and second elements of each pair in the original function. |
|
In plain English, finding an inverse is simply the swapping of the x and y coordinates.
f (x) = {(2,3), (4,5), (-2,6), (1,-5)} (function)
The inverse of f (x) = {(3,2), (5,4), (6,-2), (-5,1)} (function)
Let's look at another example: g (x) = {(4,1), (8,3), (-5,3), (0,1)} (function)
The inverse of g (x) = {(1,4), (3,8), (3,-5), (1,0)} (NOT a function, the x = 3 repeats)

This fact leads to some subtle differences in terminologies:
Definition:Inverse of a Function: The relation formed when the independent variable (x) is exchanged with the dependent variable (y) in a given relation. (This inverse may NOT be a function.)
Definition: Inverse Function:If the inverse of a function (defined above) is itself also a function, it is then called an inverse function. |

 Finding an Inverse: Finding an Inverse:
A function receives an input value, performs some operation on this value, and creates an output answer. The inverse of the function takes that output answer, performs some operation on it, and arrives back at the original function's starting input value.
A function and its inverse "undo" one another, leaving you right back where you started.
So how do we find these inverse relationships?
• Method 1 (ordered pairs):
If the function is stated as a set of ordered pairs, we can find the inverse of the function by simply swapping the ordered pairs (as seen at the top of this page).
If the definition of the function is fairly simple, we may be able to find the inverse of the function by examining selected ordered pairs and looking for a relationship for the inverse.
Let f (x) = x + 1
x |
y=f (x) |
1 |
2 |
3 |
4 |
-2 |
-1 |
0 |
1 |
|
Inverse of f (x)
x |
inverse |
2 |
1 |
4 |
3 |
-1 |
-2 |
1 |
0 |
|
It can be seen from this example that the inverse will be subtracting one from each of its input values.
Inverse of f (x) = x + 1,
or
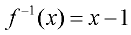
|
NOTATION:
An inverse function is denoted by
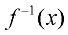 .
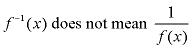
|
|
• Method 2 (algebraic):
There is a simple method to find the inverse of a function algebraically.
Process
1. Set the function = y
2. Swap the x and y variables
3. Solve for y. |
Find the inverse of function f (x) = x + 6.
1. y = x + 6
2. x = y + 6
3. x - 6 = y which is the inverse f -1 (x) = x - 6 |
• Method 3 (graphing):
The graph of an inverse relation is the reflection of the original graph over the
line y = x (called the Identity Function). It may be necessary to restrict the domain of the starting function to ensure that the inverse is also a function.
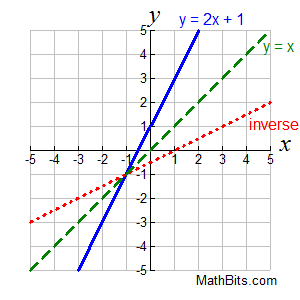
Our starting function is y = 2x + 1.
If we reflect our starting function over the identity line, y = x, we obtain the red dotted line. The new red line is our inverse of y = 2x + 1.
For this example, the inverse passes the vertical line test, making the inverse a function.
Not all graphs produce an inverse which will also be a function.
|
|

 Determine graphically if an inverse is also a function: Determine graphically if an inverse is also a function:
We know that the Vertical Line Test is used to determine if a graph represents a function.
[If a vertical line drawn anywhere on a graph only intersects the graph in one location, the graph is a function.]
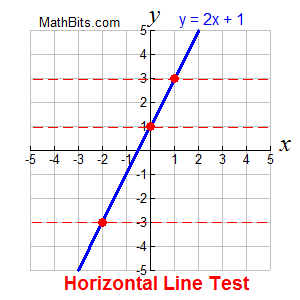
We can use a horizontal line to determine if a function will have an inverse which is also a function.
Simply draw a horizontal line anywhere on the original function. Just like the Vertical Line Test, the horizontal lines must intersect the graph in only one location.
If there is only one intersection, at any location, the graph has an inverse which is also a function. If the original function passes the Horizontal Line Test, its inverse will pass the Vertical Line Test for functions. |
|
 Restrict the domain to insure an inverse function: Restrict the domain to insure an inverse function:
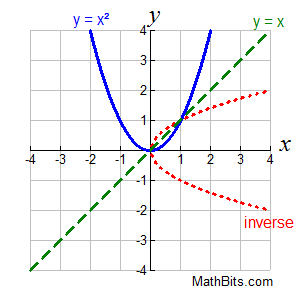
| If a horizontal line intersects the original graph in more than one location, it may be possible to restrict the domain of the original graph to ensure the inverse will be a function, and pass the Vertical Line Test for functions.
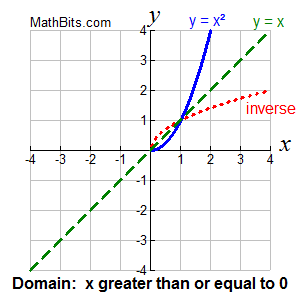
You can see that the reflection (in red) in the example at the right does not pass the Vertical Line Test. The inverse of the function y = x² is not an inverse function. The inverse relation exists, but it is not a function.
It is possible, however, to restrict the domain of y = x² to ensure that the inverse of a portion of the graph will be a function. |
|
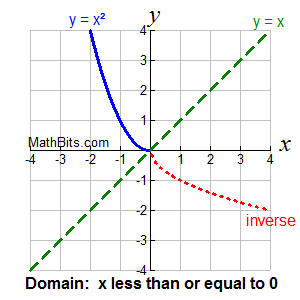
To restrict the domain, we want to cut the original function in such a way that what remains will pass the Horizontal Line Test ensuring the inverse to be a function.
Here are two possible restrictions which ensure that the inverse of y = x² will be a function for a portion of the graph. Since y = x² is a parabola, cutting the function at the turning point, (0,0), will work nicely.
Function: y = x² for x > 0
 |
Function: y = x² for x < 0
 |


NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|