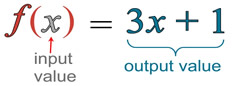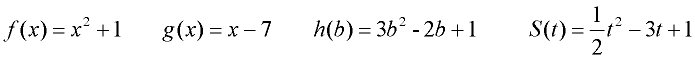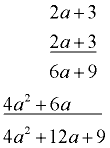|
Function notation is the way a function is written. It is meant to be a precise way of giving information about the function without a rather lengthy written explanation.
The most popular function notation is f (x) which is read "f of x".
This is NOT the multiplication of f times x.. |
|
|
"f (x)" simply replaces "y" in the equation y = 3x + 1, shown above.
Function notation tells us the "name" of the function, and the "algebraic rule" it will be using.
Traditionally, functions are referred to by single letter names, such as f, g, h and so on.
Any letter(s), however, may be used to name a function. Examples:
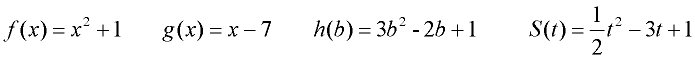 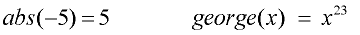
 Remember: y = f (x). Remember: y = f (x).
The f (x) notation is another way of representing the y-value in a function.
The y-axis may even be labeled as the f (x) axis, when graphing.
Ordered pairs may be written as (x, f (x)), instead of (x, y).
Note: The notation f : X → Y tells us that the function's name is "f " and its ordered pairs are formed by an element x from the set X, and by an element y from the set Y.
(The arrow → is read "is mapped to".)
|
Advantages of function notation:
1. |
it allows for individual function names to avoid confusion as to which function is being examined.
Names have different letters, such as f (x) and g (x).
The graphing calculator does distinctive function naming with Y1, Y2,
... |
2. |
it quickly identifies the independent variable in a problem. f (x) = x + 2b + c, where the variable is "x".
|
3. |
it quickly states which element of the function is to be examined. Find f (2) when f (x) = 3x, is the same as saying, "Find y when x = 2, for y = 3x." |
|
Equivalent Notations! |
y = 3x + 2 |
f (x) = 3x + 2 |
f (x) = {(x,y) | y = 3x + 2}
Set-builder notation form:
(the vertical bar is read "such that")
|
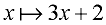 (the bar arrow means the element
(the bar arrow means the element
"x is mapped/matched to 3x + 2") |
|
|

| |
 |
|
To evaluate a function, substitute the input (the given number or expression) for the function's variable (place holder, x).
Replace the x with the number or expression.
|
1. |
Given the function f (x) = 3x - 5, find f (4).
Solution: Substitute 4 into the function in place of x. f (4) = 3(4) - 5 = 7.
This answer can be thought of as the ordered pair (4,7).
The answer may also be referred to as the image of 4 under f (x). |
2. |
Find the value of h(b) = 3b2 - 2b + 1 when b = -3.
Solution: This is function "h" with variable "b".
Substitute -3 into the function in place of b. h (-3) = 3(-3)2 - 2(-3) + 1 = 34.
|
3. |
Find g(2w) when g(x) = x2 - 2x + 1.
Solution: When substituting expressions, like 2w, into a function, using parentheses will help prevent algebraic errors. For this problem, use (2w).
g (2w) = (2w)2 - 2(2w) + 1 = 4w2- 4w +1 (Note: the answer is in terms of w.) |
4. |
Given f (x) = 2x2 + 4x - 3, find f (2a + 3).
Solution: Be sure to use parentheses!
Be careful - more algebra work is needed here.
f (2a + 3) = 2(2a + 3)2 + 4(2a + 3) - 3
= 2(4a2 + 12a + 9) + 8a + 12 - 3
= 8a2 + 24a + 18 + 8a + 12 - 3
=
8a2 + 32a + 27 |
Did you multiply?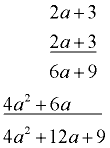 |
|
|
5. |
Given f (x) = x2 - x - 4. If f (k) = 8, what is the value of k?
Solution: Using x = k, Set the function rule equal to 8 and solve for k.
k2 - k - 4 = 8
k2 - k - 12 = 0
(k - 4)(k + 3) = 0
k - 4 = 0; k + 3 = 0
k = 4; k = -3 |
The value of k can be either 4 or -3. |
|

|
For calculator help with
evaluating expressions and functions
click here. |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|