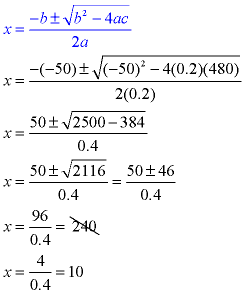|
Let's see how the Quadratic Equations can be applied in a variety of situations:

The product of two positive consecutive even integer is 360. Find the numbers using a quadratic equation. |
Notice: this question asks for "positive" answers.
Solution:
Let x = first number
x + 2 = second number
x(x + 2) = 360
x2 + 2x - 360 = 0
(x + 20)(x - 18) = 0
x + 20 = 0; x = -20 (reject as the numbers are positive)
x - 18 = 0; x = 18 (first number)
x + 2 = 18 + 2 = 20
(second number) |
"Consecutive" means "one after another", such as:
12 and 13 are consecutive integers,
3 and 5 are consecutive odd integers,
8 and 10 are consecutive even integers.
 |


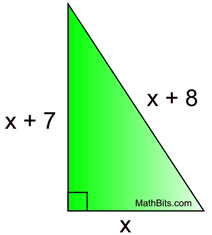
One leg of a right triangle is seven more than the other leg. The hypotenuse is eight more than the shorter leg. Find the lengths of the three sides of the triangle.
|
When working with right triangles, think of the Pythagorean Theorem.
Solution:
Let x = short leg
x + 7 = longer leg
x + 8 = hypotenuse
Apply the Pythagorean Theorem
a2 + b2 = c2
x2 + (x + 7)2 = (x + 8)2
x2 + x2 + 14x + 49 = x2 + 16x + 64
2x2+ 14x + 49 = x2 + 16x + 64
x2 - 2x + 15 = 0
(x - 5)(x + 3) = 0
x - 5 = 0; x = 5
x + 3 = 0; x = -3 (reject as lengths are not negative)
x = 5
x + 7 = 12
x + 8 = 13 |
Check
in Pythagorean Theorem:
52 + 122 = 132
25 + 144 = 169
169 = 169 check
|


The width of a rectangle is four less than its length. The area of the rectangle is 192 square units. Find the length and width of the rectangle. |
Pick out the key words in a problem. The word AREA stands out as a key word.
Use algebraic expressions to represent the sides. |
Solution:
Let x = the length
x - 4 = the width
Remember, the key word is AREA.
Area = x(x - 4) = 192
x2 - 4x = 192
x2 - 4x - 192 =0 (either factor or use the quadratic formula)
(x - 16)(x + 12) = 0
x - 16 = 0; x = 16
x + 12 = 0; x = -12 (length is not negative)
x - 4 = 12 |

Dimensions: 16 x 12
|


A store's revenue from selling skateboards is determined by multiplying the number of skateboards by the cost per skateboard. The revenue, r, from selling x skateboards (where x is less than or equal to 50) is r = x(50 - 0.2x). How many skateboards need to be sold to have a revenue of $480. |
When a formula (equation) is given within the problem, use the formula.
The problem generally requires you to substitute values into the formula and solve for some value.
Solution:
Set the formula equal to $480.
480 = x(50 - 0.2x)
480 = 50x - 0.2x2
0.2x2 - 50x + 480 = 0 (use quadratic formula)
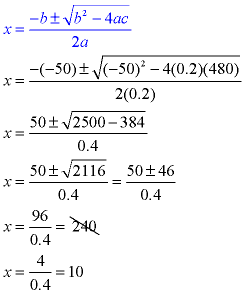
|

Since the problem stated that x was less than or equal to 50, reject the solution of 240.
They must sell 10 skateboards to have a revenue of $480. |


The Allen family has installed a rectangular in-ground swimming pool. There is a concrete sidewalk around the pool with a consistent width of x feet. The outside edge of the sidewalk measures 24 feet by 41 feet. If the area of the pool is 630 square feet, find the width of the sidewalk. |
Draw a diagram to get a better understanding of the situation.
Solution:
Since we know the "area" of the pool, let's start with area.
The area of the pool can be expressed as:
(24 - 2x)(41 - 2x) = 630
984 - 48x - 82x + 4x2 = 630
4x2 - 130x + 354 =0 (factor or quadratic formula)
2x2 - 65x + 177 = 0
(2x - 59)(x - 3) = 0
2x - 59 = 0; x = 29.5 ft (not realistic sidewalk width)
x - 3 = 0; x = 3 feet (acceptable sidewalk width) |
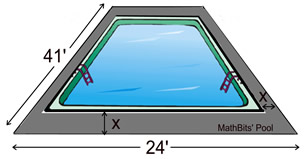
[When determining the expressions to represent the sides of the pool, be sure to subtract the sidewalk width twice - once from each side of the pool.
24 - 2 x and 41 - 2 x ] |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|