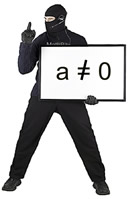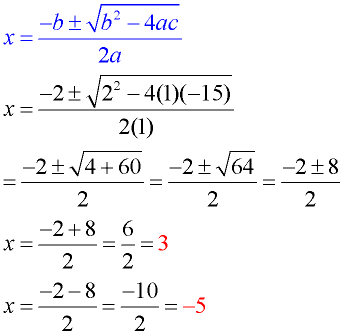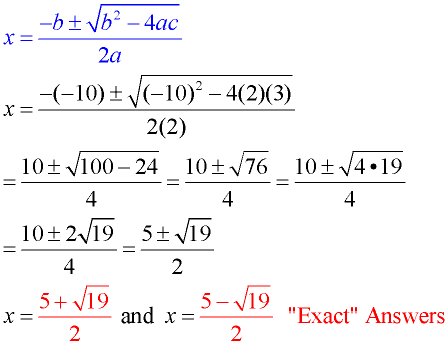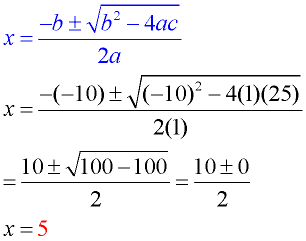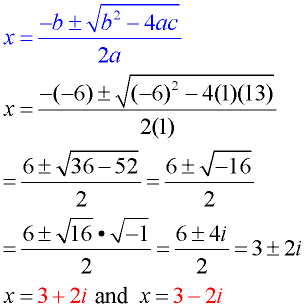The solutions for some quadratic equations are not rational, and cannot be obtained by factoring.
Let's see the Quadratic Formula at work in various situations:
Topical Outline | Algebra 1 Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|