Summary of Facts on this Page:
• The sum of two rational numbers is rational.
• The product of two rational numbers is rational.
• The sum of two irrational numbers is SOMETIMES irrational.
• The product of two irrational numbers is SOMETIMES irrational. |
 |
|

 "The sum of two rational numbers is rational."
"The sum of two rational numbers is rational."
By definition, a rational number can be expressed as a fraction with integer values in the numerator and denominator (denominator not zero). So, adding two rationals is the same as adding two such fractions, which will result in another fraction of this same form. Remember that integers are closed under addition, i.e. if you add two integers, you get another integer. Thus, adding two rational numbers produces another rational number.
Examples:
Proof:
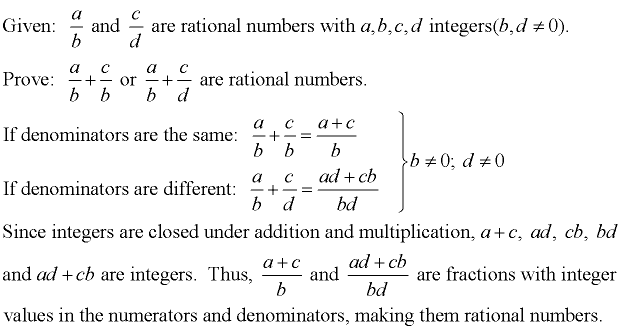

 "The product of two rational numbers is rational."
"The product of two rational numbers is rational."
Again, by definition, a rational number can be expressed as a fraction with integer values in the numerator and denominator (denominator not zero). So, multiplying two rationals is the same as multiplying two such fractions, which will result in another fraction of this same form. Remember that integers are closed under multiplication, i.e. if you multiply two integers, you get another integer.
Thus, multiplying two rational numbers produces another rational number.
Examples:
Proof:



Look out! This next part gets tricky!!
 "The sum of two irrational numbers is SOMETIMES irrational."
"The sum of two irrational numbers is SOMETIMES irrational."
The sum of two irrational numbers, in some cases, will be irrational. However, if the irrational parts of the numbers have a zero sum (cancel each other out), the sum will be rational.
Examples:
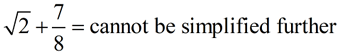 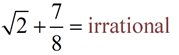 Remember, the square root of two is irrational and cannot be expressed as a fraction.
Remember, the square root of two is irrational and cannot be expressed as a fraction.
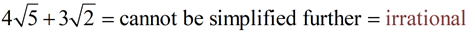
 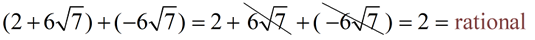 The irrational portions of this sum cancel each other out (have a zero sum), leaving only the rational value.
The irrational portions of this sum cancel each other out (have a zero sum), leaving only the rational value.
|

 "The product of two irrational numbers is SOMETIMES irrational."
"The product of two irrational numbers is SOMETIMES irrational."
The product of two irrational numbers, in some cases, will be irrational. However, it is possible that some irrational numbers may multiply to form a rational product.
Examples: