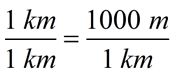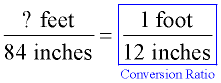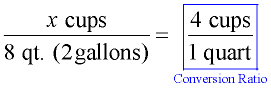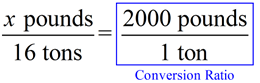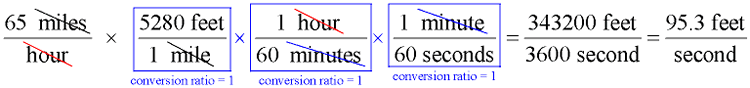Metric System: Metric System: |
|
|
The metric system is an internationally agreed decimal system of measurement created in France in 1799. The International System of Units (SI), the official system of measurement in almost every country in the world, is based upon the metric system. |
In the metric system, each basic type of measurement (length, weight, capacity) has one basic unit of measure (meter, gram, liter). Conversions are quickly made by multiplying or dividing by factors of 10. It is as simple as moving the decimal point to the right (for smaller prefixes) or to the left (for larger prefixes).
To remember the proper movement, arrange the prefixes from largest to smallest.


Kilo means thousand (1000)
Hecto means hundred (100)
Deca means ten (10) |
Deci means one-tenth (1/10)
Centi means one-hundredth (1/100)
Milli means one-thousandth (1/1000) |
Length:
1 kilometer (km) = 1000 meters
1 centimeter (cm) = .01 meter
1 millimeter = .001 meter (m) |
Weight:
1 kilogram (kg) = 1000 grams (g)
1 milligram (mg) = .001 gram |
Capacity:
1 milliliter (ml)= .001 liter (l)
|

Conversion Ratio (or Unit Factor): A conversion ratio (or unit factor) is a ratio equal to one. This ratio carries the names of the units to be used in the conversion. It can be used for conversions within the English and Metric Systems, as well as for conversions between systems. The conversion ratio is based upon the concept of equivalent values. In the example below, 1000 meters is substituted for its equivalent measure of 1 kilometer.
|
Proportions will help you make conversions
when working with measurements.
Create a unit conversion ratio, which is always equal to 1: 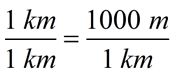 |

 Convert 10.25 kilometers to meters. Convert 10.25 kilometers to meters.
Notice in the listing above that meter is three places to the right of the prefix kilo. This tells us to move the decimal point three places to the right. The answer is 10,250 meters.
 |
(Problem using
dimensional analysis) |
Convert 4.5 kilometers to millimeters.
1 km = 1,000,000 mm
|
|
 Convert 650 mL to daL. [mL is milliliters and daL is decaliters]. Convert 650 mL to daL. [mL is milliliters and daL is decaliters].
Notice in the listing above that the prefix deca is four places to the left of the prefix milli. This tells us to move the decimal point four places to the left. The answer is 0.0650 daL. (Note: dL is deciliters, daL is decaliters.)
 Convert 750 grams to milligrams. Convert 750 grams to milligrams.
Notice in the listing above that the prefix milli is three places to the right of gram. This tells us to move the decimal point three places to the right. The answer is 750,000 milligrams.
 (square units) (square units)
Convert 1 km2 to m2.
|
|
 English System: English System: |
|
|
While the metric system was lawfully accepted for use in the United States in 1866, the US has not adopted the metric system as its "official" system of measurement.
| The US English System of measurement grew out of the manner in which people secured measurements using body parts and familiar objects. For example, shorter ground distances were measured with the human foot and longer distances were measured by paces, with one mile being 1,000 paces. Capacities were measured with household items such as cups, pails (formerly called gallons) and baskets. |
 |
Obviously this system allowed for discrepancies between measurements obtained by different individuals. A standard was eventually set to ensure that all measurements represented the same amount for everyone.
Length:
1 foot (ft) = 12 inches (in)
1 yard (yd) = 3 feet
1 mile (mi) =
5280 feet
1 mile = 1760 yards |
Weight:
1 pound (lb) = 16 ounces (oz)
1 ton =
2000 pounds |
Capacity:
1 tablespoon (tbsp) = 3 teasponns (tsp)
1 cup (c) = 16 tablespoons
1 cup = 8 fluid ounces (oz)
1 pint (pt) = 2 cups
1 quart (qt) = 2 pints
1 gallon (gal)
= 4 quarts
|

Conversion Ratio (or Unit Factor): A conversion ratio (or unit factor) is a ratio equal to one. This ratio carries the names of the units to be used in the conversion. It can be used for conversions within the English and Metric Systems, as well as for conversions between systems. The conversion ratio is based upon the concept of equivalent values. In the example below, one foot is substituted for its equivalent measure of 12 inches.
While the Metric System simply moves the decimal point to convert between its measurements' prefixes, the English System requires a conversion ratio (or unit factor) to move between measurements. In the Metric System, the prefix itself gives the needed conversion ratio.
|
Proportions are used when working with conversions.

|

 Convert 84 inches to feet. Convert 84 inches to feet.
A proportion can be set up using the appropriate conversion ratio. In a proportion the product of the means equals the product of the extremes. Use this "cross multipy" concept to find the answer. |
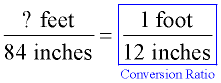 ANSWER: 7 feet
ANSWER: 7 feet
|
|
 Find the number of cups in two gallons. Find the number of cups in two gallons.
There is no stated conversion for cups to gallons, so we have to be a bit more creative. Since there are 4 cups in 1 quart, and 4 quarts in 1 gallon, we can set up the conversion ratio based on "quarts". Two gallons is 8 quarts. |
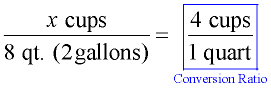 ANSWER: 32 cups
ANSWER: 32 cups
|
|
 Convert 16 tons to pounds. Convert 16 tons to pounds.
Set up the conversion ratio and solve for the missing value. |
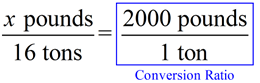 ANSWER: 32,000 pounds
ANSWER: 32,000 pounds |
|
 (multiple factors) (multiple factors)
Convert 65 miles per hour to feet per second.
|
Notice the need for 3 conversion ratios (all of which equal 1).
All units cancel out except for the desired units.
|
|
NOTE: As with all mathematical problems, there are other ways to arrive at these answers. Most other methods utilize the concept of the conversion ratio, but may be written in a different manner or calculated mentally.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|