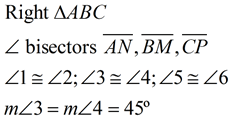We are now going to take a look at another triangle center called the
incenter.
|
A point of concurrency is the point where three or more lines intersect. |
|
We have already seen how to construct a circle inscribed in a triangle.
This discussion will focus on the name given to that point where the angle bisectors
in that construction intersect. That point is called the incenter.
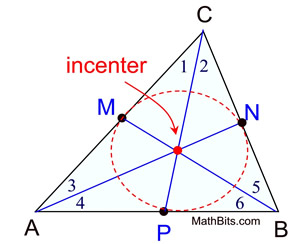
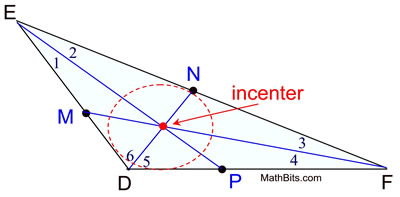
Incenter - point of concurrent angle bisectors
The three angle bisectors of the angles of a triangle are concurrent, meaning they
intersect on one common point. That common point is called the incenter of the triangle.
We know that common point is also the center of a inscribed circle tangent to all of
the sides of the triangle. Since the radii of the circle are congruent, the center
(the incenter) is equidistant from the circle's points of tangency with the sides
of the triangle.
The point of concurrency, the incenter, is always located in the interior of the triangle.
Let's take a look at the locations of the incenters in relation to
acute triangles, obtuse triangles and right triangles .
NOTE: The point of concurrency of the angle bisectors of a triangle (the incenter) is the center of an inscribed circle within the triangle. |
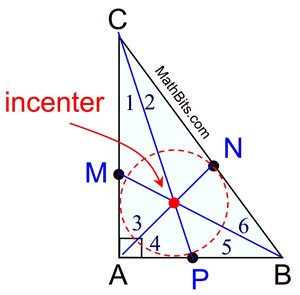
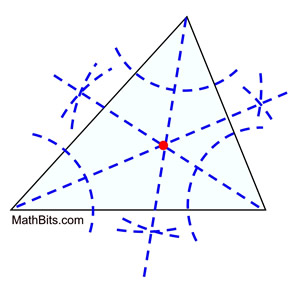
To construct the incenter:
Simply construct the angle bisectors of the three angles. The point where the angle bisectors intersect is the incenter.
|
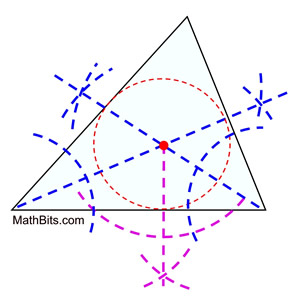
To construct the incircle:
Locate the incenter (shown at the left). Construct a perpendicular to one side of the triangle from the incenter, to determine the radius of the incircle. Draw the incircle tangent to the three sides of the triangle.
|
