 |
Remember -- use your compass
and straightedge only! |
|
A construction associated with "copying a segment" requires that you have a "place" to begin your copy. It is customary to draw a straight line upon which you then produce your copy. Such a line is called a "reference line".
| |
This construction may also be known as "Constructing a Congruent Segment", |
Given: 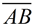 (a line segment) (a line segment)
Construct: a line segment congruent to 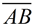 . .
(make a copy of the segment). |
 |
STEPS:
1. Using a straightedge, draw a reference line, if one is not provided.
2. Draw a dot on the reference line to mark your starting point for the construction.
3. Place the point of the compass on point A on the given figure.
4. Stretch the compass so that the pencil is exactly on B. Make a small arc through B.
(This small arc will show that you measured the length of the segment with your compass.)
5. Without changing the span of the compass, place the compass point on the starting point (dot) on the reference line and swing the pencil to create an arc crossing the reference line.
6. Label your copy.
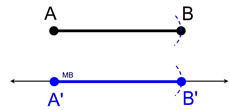
Proof of Construction: Following this construction, 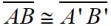 since since 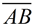 and and 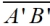 are radii of congruent circles. (The construction shows only an "arc" of the circle, but the complete circle still exists.) are radii of congruent circles. (The construction shows only an "arc" of the circle, but the complete circle still exists.)

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|

