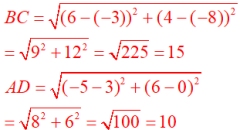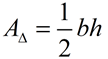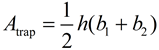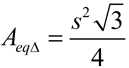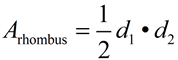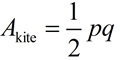GeometrySmallLogo
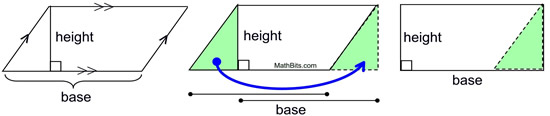
The formulas on this page should look familiar, as they pertain to triangles and quadrilaterals.
The discussion, however, will extend to the derivations of the basic formulas.

def
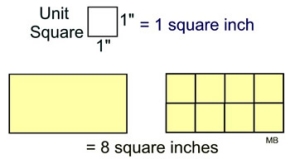
Area is the quantity that expresses the amount of surface a two-dimensional shape covers in square units. The area of a shape can be measured by comparing the shape to squares of a fixed size.

The example at the left shows a rectangle divided into 8 unit squares where each unit square represents 1 square inch.

There are two rows of four unit squares.

The area of the rectangle is 8 square inches.

divider

The examples below utilize a variety of geometry concepts to determine area.


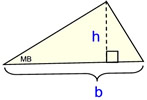
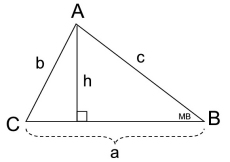
1. Find the area of ΔABC using the formula
A = ½bh.

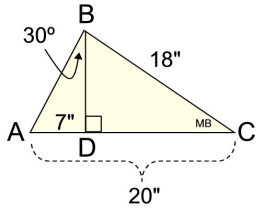
Solution: We need to find the missing altitude from B to D for the formula A=½bh..
ΔABD is a 30º-60º-90ºΔ, where the side opposite the 30º angle will be half of the hypotenuse. Since 7 is half of 14, we know that the hypotenuse from A to B equals 14".
Now, BD (long leg) will be ½ of that hypotenuse times radical 3.


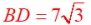
(answer in square units)

 

2. Find the area of ΔABC using the formula
A = ½ab sinC. Round to nearest hundredth.

Solution: We no longer need to find the altitude. We have all we need for this formula.
A = ½ • a • b • sinC
A = ½ • 32 • 35 • sin44º =389.0086875
Area = 389.01 square units.

 

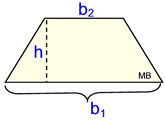
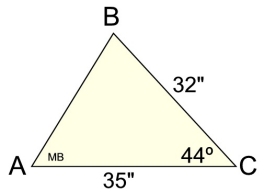
3. Find the area of trapezoid TRAP.

Solution: trap formula: A = ½h(b1 + b2).
We have all we need.
A = ½ • 4 • (6 + 9) = 30 square units.
If you forget the area formula for a trapezoid, you can partition the diagram into a rectangle and a triangle.
Area rectangle = 6 • 4 = 24
Area 3-4-5 rt.triangle = ½ • 3 • 4 = 6
Total area = 30 square units..


4. Find the area of ΔABC to the nearest tenth.

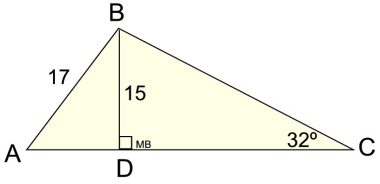
Solution: BD is given, but we need to find base AC for the formula A = ½bh.
ΔABD is a Pythagorean triple right Δ
(8-15-17), so AD = 8.
We need to use trigonometry. to find DC.
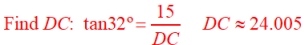
AC = 8 + 24.005 = 32.005
Area = ½ • 32.005 • 15 = 240.0375
= 240.0 square units

 

5. Find the area of ΔABC using Distance Formula and your knowledge of equations of lines. Use the side from B to C as the base, with the altitude starting at A.

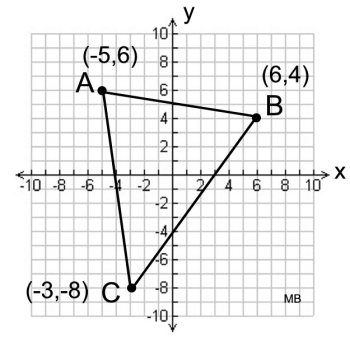
Solution: We need to find point D, where the altitude will cross the base to get AD.
The slope of the base is 4/3 so the slope of the altitude will be -3,4. By counting "rise" and "run", D is at (3,0). It checks in the equation of the base: y = (4/3)x - 4.
Using the Distance Formula:

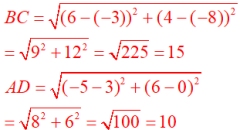
Area: ½ • 15 • 10 = 75 square units

divider


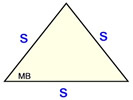
Derivations of well known area formulas of 3 and 4-sided polygons:

Rectangle
arearect
   area3    
Due to the perpendicular nature of rectangles, "unit squares" can be easily used to tile the rectangle's surface to represent the area. The unit squares can be subdivided to represent fractional lengths if needed. It can be observed that the area is found by multiplying the dimensions of the rectangle.

base b = a side of the rectangle
height h = a side that is perpendicular to the base
Parallelogram
areapara
area5      
A parallelogram can be thought of as a slanted rectangle. It can be decomposed to create a triangle from the slanted portion which can be translated to the opposite side, creating a rectangle.
parallelogramtrio

Triangle
areat  area1

 
The area of a triangle is related to the area of a rectangle. Consider 3 cases:
triangleduo
ΔA congruent to ΔB
area rectangle = areas ΔA + ΔB
bh = area ΔA + area ΔA
bh = 2(area ΔA)
½bh = area ΔA
ΔA congruent to ΔA1
ΔB congruent to ΔB1
area rectangle =
    areas ΔA+ΔB+ΔA1+ΔB1
bh = areas ΔA+ΔB+ΔA+ΔB
bh = 2(area ΔA+ΔB)
½bh = areas ΔA+ΔB =
    area given blue Δ
obtusetwo
Drawing a rectangle around triangle A will be counterproductive since the base of the triangle will no longer be the base of the rectangle. Instead, draw the rectangle to coincide the bases. The height of the triangle is the same as the height of the rectangle. Triangle B has the same area as triangle A (same base and height). We showed scalene triangles like B have area = ½bh.
Trapezoid
areatrap
area7
A trapezoid is a composite figure made up of other geometric shapes. Partition the figure to form 2 triangles and one rectangle.
area trap = area ΔA + area rect. C + area ΔB
area trap = ½xh + b1h + ½yh
= b1h + ½h(x + y)
= b1h + ½h(b2 - b1)
= b1h + ½b2h - ½ b1h
= ½b1h + ½b2h
= ½h( b1+ b2)		 traptwoa

Area of a Triangle
(trigonometric formula)


Other formulas: (Remember "regular" means all sides of equal length, and all angels of equal measure.)

"Regular" Triangle
(Equilateral Δ )
areaeqt
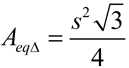area2
"Regular" Quad
(Square)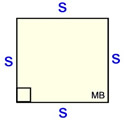
areasq
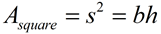area4
Rhombus

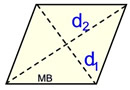
arearhom
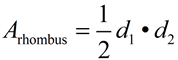area6
Kite

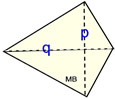
areakite
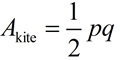area8

divider

tidbit When considering perimeter and area of a figure, is it true that as the area gets larger, the perimeter also gets larger?

If you are dealing with an enlargement (a dilation) of a figure, increasing the area will also increase the perimeter.

You cannot, however, generalize this result by stating that "increasing the area of a figure will always increase the perimeter of the figure". Consider the image at the right. The area of the pentagon is decreased by cutting chunks away, but the perimeter is increased.
Small triangular sections are cut out of the pentagon on the left (see arrow), so the remaining shape looks like 6 small pentagons.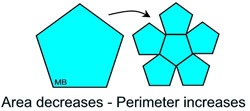cutUpPent


divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".