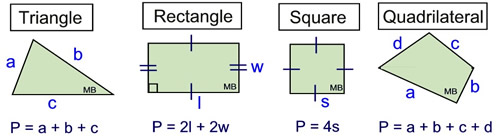
Shown below are some familiar perimeters expresses as "formulas".
While perimeter sounds like a simple concept, it can be challenging when a question requires the use of past skills such as the Pythagorean Theorem, trigonometry, special right triangle formulas, the distance formula, or other concepts, to find lengths of individual segments.
Topical Outline | Geometry Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|

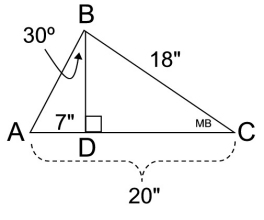
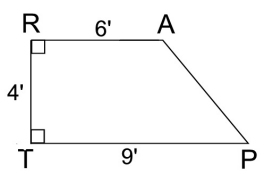
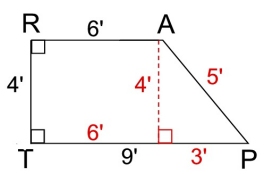
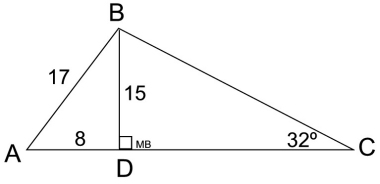
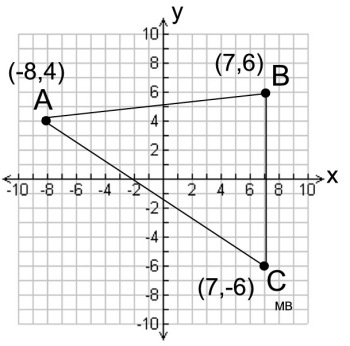
 Perimeter of ΔABC:
Perimeter of ΔABC: