Area of Circle

 

Like circumference, the area of a circle also deals with pi (π).
A = π • r²
A = area of circle, r = radius

Half of a circle is called a "semicircle".

From our work with circumferences of circles, we know that the definition of circumference is associated with the "perimeters" of inscribed polygons. In a similar manner, the definition of the area of a circle is also associated with the "areas" of inscribed polygons.
(See Archimedes' investigation at the bottom of this page.)

The area of a circle is the limit of the "areas" of the inscribed regular polygons as the number of sides increases without bound.

The following examples employ skills you have encountered in Geometry.

1. This figure is composed of a semicircle and a right triangle. Find the area of the total figure, rounded to the nearest tenth of a square foot.

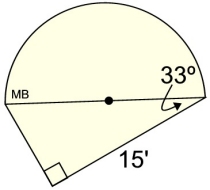
Solution: There are several solution methods. This is one solution. • Trigonometry is needed to find the hypotenuse of the right triangle. • Area of Δ = ½ ab sin C = ½ (15)(17/885) sin(33º) = 69.441 sq. ft. • radius of semicircle = ½(17.885) = 8.9425 Area semicircle = ½πr2 = ½π(8.925)2 = 125.644 sq. ft. • Total Area = 69.441 + 125.644 = 195.085 = 195.1 square feet

 

2. Given circle O, with semicircles O, A and B. Find the area of the shaded (colored) region in terms of π.

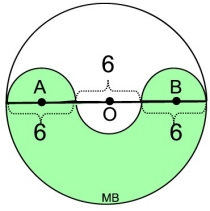
Solution: There are several ways to attack this problem. This is one solution method. • Find the area of half of the large circle O containing the majority of the green color. A =½πr2 = ½π92 = ½81π = 40.5π. • All of the small semicircle are of the same size. Find the area of one. A =½πr2 = ½π32 = ½9π = 4.5π. • From our large green semicircle, we need to add on two small green semicircles and remove one white semicircle. Or just add one small green semicircle. 40.5π + 4.5π = 45π.

 

3. Given the equation of a circle to be      x2 + y2 + 8x - 12y + 36 = 0, a) find the center and radius of the circle. b) find the area of the circle expressed in terms of pi, and also rounded to the nearest tenth.

Solution: a) Complete the square: b) Area = πr2 = 64π square units or Area = 201.1 square units

Derivation of the Area Formula:
As was the case with circumference, the "formal" derivation (proof) of the area formula also involves calculus integration, which is beyond the scope of this course. We can, however, visualize the creation of the circle area formula, and examine Archimedes' investigation based upon geometry.

Method 1: Visualization:
Let's look at a visualization of the area formula (you saw this approach in previous courses),

We start knowing that the circumference of a circle is C = 2π • r, and that the area of a rectangle is A = bh.

A circle is divided into congruent sectors (pie slices). The sectors are pulled out of the circle and are arranged as shown in the middle diagram below. The length across the top (over the curved blue arcs) is half of the circumference, with the length across the bottom (over the curved gold arcs) being the other half of the circumference.

When placed in these positions, the sectors can be outlined by a parallelogram. The larger the number of sectors that are cut, the less curvy the arcs will appear and the more the shape will resemble an actual parallelogram. As seen in the third diagram below, the parallelogram can be changed into a rectangle by slicing half of the last sector and placing it to the far left.

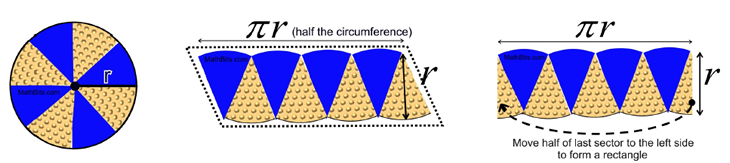
The area of the rectangle is A = bh.
Thus, the area of the sectors that make up the rectangle is πr • r = π • r².