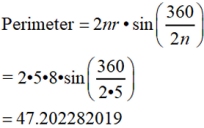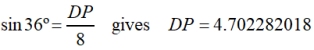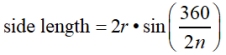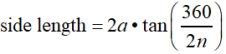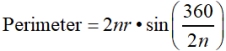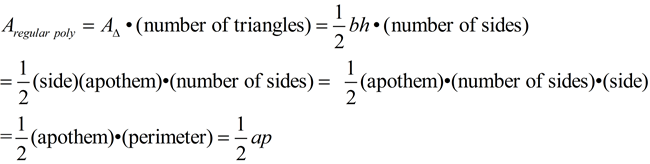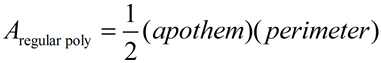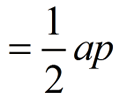Remember that "regular" polygons have all sides congruent and all angles congruent.
Regular polygons have a center and a radius (coinciding with their circumscribed circle),
and the distance from the center perpendicular to any side is called its apothem.
(You may see "apothem" referred to as "height".)
Regular Pentagon |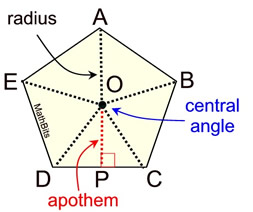
The apothem of a regular polygon is a line segment from the center of the polygon perpendicular to any side of the polygon.
Δ DOC is an isosceles triangle, making the apothem the altitude of this triangle and the median of this triangle (going to the midpoint P.)
ΔDOC is one of five congruent triangles inside the regular pentagon.
(ΔAOB, ΔBOC, ΔCOD, ΔDOR, ΔEOA) |
Note how angles can come into play in these popular regular polygons.
Along with finding the central angle, we can also use the equation from the last lesson
to find an interior angle. In the diagram above, ∠OBC is an interior angle.
(Remember: The formula for each interior angle of a regular polygon is [180(n - 2)] /n where n = the number of sides.).
Central angle = vertex at the center of polygon. Interior angle = vertex at a vertex of the polygon.
Equilateral Triangle
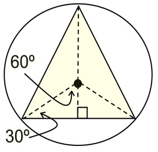central angle = 120°
interior angle = 60º
Special 30º-60º-90º Δs
at work!
|
Square
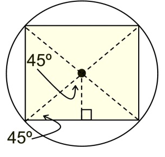central angle = 90º
interior angle = 90º
Special 45º-45º-90º Δs
at work!
|
Regular Pentagon
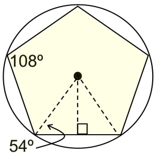central angle = 72º
interior angle = 108º
Must use trig. to
work in this triangle.
|
Regular Hexagon
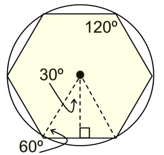central angle = 60º
interior angle = 120º
Special 30º-60º-90º Δs
at work! |
Regular Octagon
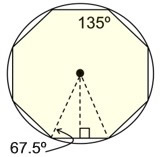central angle = 45º
interior angle = 135º
Must use trig. to
work in this triangle.
|
|
PERIMETER:
The difficulty associated with finding perimeter is based upon what information you are given regarding the polygon. For example, if you are given the length of a side of a regular polygon, all you need to do is multiply the length by the number of sides to find the perimeter. It is, however, unlikely that a question will be that simple in a Geometry course.
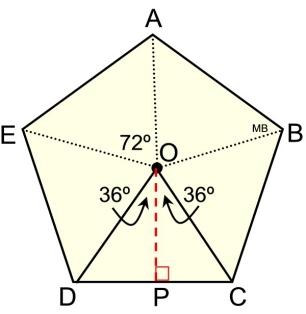
A crucial area on which to focus, when working with regular polygons, is the isosceles triangle formed by the radii of the polygon and one of its sides. Let's take a look at ΔDOC from the regular pentagon shown at the beginning of this page.
In a regular pentagon (5 sides), with a given radius = 8 inches, find the perimeter.
• isosceles ΔDOC with OD = OC = 8"
• the central angle (∠DOC) = 360/n = 360/5 = 72º
(n = number of sides)
• m∠DOP = m∠COP = 36º
• apothem (or "height" or "altitude") of ΔDOC from point O to point P.
To find the perimeter, we need to know the length of one side of the pentagon, such as DC.
Using right triangle trigonometry, we can find DP.
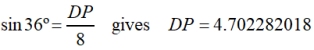
(full calculator display)
DP = ½ DC, hence DC = 9.404564037
Perimeter = 5 • DC |
regular pentagon
Perimeter = 5 • 9.404564037
= 47.02282019
=47.023
inches
(rounded to 3 decimal places) |
There are three formulas for working with regular polygons that can be helpful, when finding:
• the length of a side given the radius
• the length of a side given the apothem
• the perimeter given the radius
NOTE: It is unlikely that you will remember these formulas since they are only used occasionally.
If you follow the strategy shown in working with the pentagon above, you will be able to solve the problem without these formulas.
Let's check out the third formula for perimeter to see if it matches our previous answer:
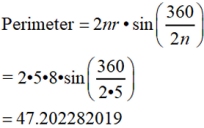( matches the answer found without the formula)
AREA:
We saw under the "perimeter" section how to go about finding missing information about a regular polygon by examining the isosceles triangle formed by the radii of the polygon and one of its sides. This triangle will also be the key to finding the area of a regular polygon. When working with "area", we will be focused on the altitude, and the side of that isosceles triangle.
Regarding these isosceles triangles, such as ΔDOC, we know:
• the number of triangles = the number of sides of the regular polygon
•
the triangles are congruent to one another
Thus, if we know the area of one triangle, we will know the area of the entire polygon. |
In a regular pentagon (5 sides), with a given radius = 8 inches, find the area.
(round to nearest integer)
To find the Δ's area, we need to find the base of isosceles ΔDOC and its altitude (apothem) from O to P.
Use trigonometry:
• Find DP:
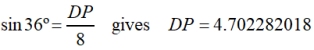
DP = ½ DC, hence side DC = 9.404564037
• Find OP:
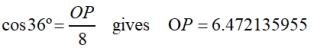
altitude (apothem) OP = 6.472135055
Area
ΔDOC = ½(9.404564037)(6.472135055)
= 30.43380852 square units.
Area of pentagon = 5 • area of
ΔDOC = 152 sq,in. |
regular pentagon
Area of pentagon =
the sum of the areas of
the 5 congruent triangles.
|
Is there a "formula" for the area of a regular polygon?
Yes! We just saw that using the strategy of partitioning, the areas of regular polygons can be found by adding together the areas of all of the congruent triangles formed by the central angles and each side of the polygon. This will be the basis for an area formula.
Remember: the area of a triangle is A= ½bh. When dealing with a polygon, the "base" will be a "side of the polygon" and the "height" will be the "Δ's altitude (which is the polygon's apothem).
| The apothem of a regular polygon is a line segment from the center of the polygon perpendicular to any side of the polygon. |
With a series of substitutions, we can arrive at a formula.
Remember that the number of congruent triangles = the number of sides of the polygon.
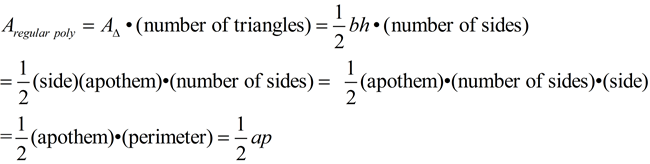
Area of a
REGULAR polygon |
|
(where a = apothem and p = perimeter) |
|
| Let's take another look at the area of regular pentagon ABCDE. This time, let's apply the new formula.
Triangle DOC is an isosceles triangle in which the triangle's altitude is the polygon's apothem (from O to P).
As was done in the previous example, we find DC and OP using trigonometry.
side: DC = 9.405
apothem: OP = 6.472
The area = ½ ap = ½ (6.472)(47.025)
A = 152 sq. in.
(rounded to nearest integer) |
Regular Pentagon
radius = 8 inches |
|
In addition to using the strategy of partitioning, it may also be possible to graph the polygon on a set of coordinate axes and determine the area using coordinate geometry techniques. A "grid" method may be useful if sufficient information is known. |
|
