|
A polygon is a 2-dimensional closed figure that is the union of line segments in a plane. A polygon has three or more sides. |
|
Geometry establishes a solid foundation for working with 3-sided and 4-sided polygons.
In Junior Math, the concept of "additional polygons" was introduced.
This section will refresh those concepts, and add some new information.
The emphasis will be on "regular" polygons.
Classifications of Polygons |
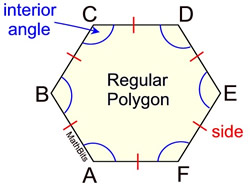
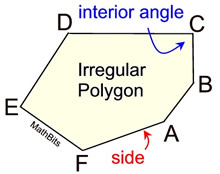
• Polygons can be classified as either regular or irregular.
In a regular polygon, all of its interior angles are of the same measure and all of its sides are the same length.
|
In an irregular polygon, the interior angles may be of different measures and the sides may be different lengths.
|
A polygon that is regular is both equilateral AND equiangular.
A regular triangle is an equilateral triangle (and an equiangular triangle).
A regular quadrilateral is a square. |
 |
The term "polygon" refers to a type of figure which may be regular or irregular. Do NOT assume "polygon" means "regular polygon". If a polygon is a regular polygon, it will be stated as such. |
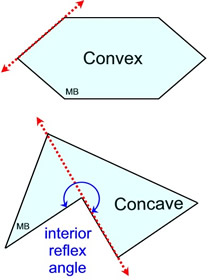
• Polygons can be classified as either convex or concave.
A polygon is convex if no line that contains a side of the polygon contains a point in the interior of the polygon. In a convex polygon, each interior angle measures less than 180 degrees. A triangle is always convex, and regular polygons are always convex.
Concave polygons "cave-in" to their interiors, creating at least one interior angle greater than 180 degrees (a reflex angle).
Our emphasis will be on concave polygons.
|
|
Parts of Regular Polygons |
Regular Pentagon
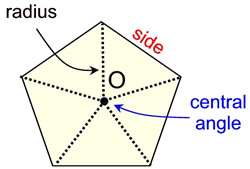The black dot is the center of the polygon. |
The center, (O), of a regular polygon, is a point in the interior of the polygon equidistant from each vertex. It is also the center of the inscribed and circumscribed circles. The radius is the distance from the center to any vertex.
The central angle of a regular polygon is formed by connecting the center to two adjacent vertices. All central angles are of equal measure inside one regular polygon. The number of central angles = the number of sides.
Each central angle = 360/n (n = number of sides). |
Irregular polygons are not described as having a "center" which is equidistant from each vertex. As such, an irregular polygon does not have central angles or radii. An irregular polygon does, however, have a center of gravity or a centroid. |
Types of Regular Polygons |
The table below shows some of the more commonly used regular polygons.
Polygon |
Figure |
Sides |
Angles |
Diagonals |
Number Δs
from 1 vertex |
Regular Triangle
(Equilateral)
|
|
3 |
3 |
0 |
1 |
Regular
Quadrilateral
(Square)
|
|
4 |
4 |
2 |
2 |
Regular
Pentagon |
|
5 |
5 |
5 |
3 |
Regular
Hexagon |
|
6 |
6 |
9 |
4 |
Regular
Heptagon or Septagon |
|
7 |
7 |
14 |
5 |
Regular
Octagon |
|
8 |
8 |
20 |
6 |
Regular
Nonagon or Novagon |
|
9 |
9 |
27 |
7 |
Regular
Decagon |
|
10 |
10 |
35 |
8 |
Regular
Dodecagon |
|
12 |
12 |
54 |
10 |
Regular
n-gon |
---- |
n |
n |
½n(n - 3) |
(n - 2) |
An n-gon is a polygon with n sides.
Starting with the pentagon, take a look at the "shapes" of the polygons
as the number of the side increases.
As the number of sides increases, the "shapes" of these regular polygons
approaches the "shape" of a circle.
