|
TRAPEZOID:
|
A trapezoid is a quadrilateral with at least one pair of parallel sides. |
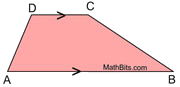 |
|
The median of a trapezoid is a segment joining the midpoints of the legs of the trapezoid.
(At the right, 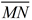 is the median for
trapezoid ABCD.) |
 |
The theorems will be stated in "if ...then" form. Both the theorem and its converse
(where you swap the "if" and "then" expressions) will be examined.
Click  in the charts below to see each proof. in the charts below to see each proof.
While one method of proof will be shown, other methods are also possible.
|
Definition and Theorems pertaining to a trapezoid: |
DEFINITION: A trapezoid is a quadrilateral with at least one pair of parallel sides. |
|
THEOREM: The median of a trapezoid is parallel to the bases and half the sum of the lengths of the bases.
|
|
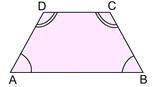
ISOSCELES TRAPEZOID
|
A isosceles trapezoid is a trapezoid with congruent base angles. |
 |
|
Note: The definition of an isosceles triangle states that the triangle has two congruent "sides".
But the definition of isosceles trapezoid stated above, mentions congruent base "angles", not sides (or legs). Why not?
If an
"inclusive"
isosceles trapezoid is defined to be "a trapezoid with congruent legs",
a parallelogram will be an isosceles trapezoid. If this occurs, the other properties that an isosceles trapezoid can possess can no longer hold,
since they will not be true for a parallelogram.
|
If, however, we define an isosceles trapezoid to be a "trapezoid with congruent base angles", the legs can be proven congruent, a parallelogram will NOT be an isosceles trapezoid, and all of the commonly known properties of an isosceles trapezoid will remain true.
|
Definition and Theorems pertaining to an isosceles trapezoid: |
DEFINITION: An isosceles trapezoid is a trapezoid with congruent base angles. |
|
THEOREM: If a quadrilateral (with one set of parallel sides) is an isosceles trapezoid, its legs are congruent. |
|
|
|
THEOREM: If a quadrilateral is an isosceles trapezoid, the diagonals are congruent. |
|
|
|
THEOREM: (converse) If a trapezoid has congruent diagonals, it is an isosceles trapezoid. |
|
|
|
THEOREM: If a quadrilateral is an isosceles trapezoid, the opposite angles are supplementary. |
|
|
|
THEOREM: (converse) If a trapezoid has its opposite angles supplementary, it is an isosceles trapezoid. |
|
|
|
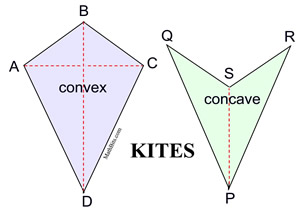
KITE
|
A kite is a quadrilateral whose four sides are drawn such that there are two distinct sets of adjacent, congruent sides. |
|
Note: Kites discussed on this page are convex kites.
|
Definition and Theorems pertaining to a kite: |
DEFINITION: A kite is a quadrilateral whose four sides are drawn such that there are two distinct sets of adjacent, congruent sides. |
|
|
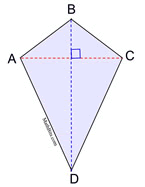
THEOREM: If a quadrilateral is a kite, the diagonals are perpendicular.

|
 |
|
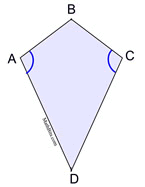
THEOREM: If a quadrilateral is a kite, it has one pair of opposite angles congruent.

|
 |
|
THEOREM: If a quadrilateral is a kite, it has one diagonal forming two isosceles triangles.

|
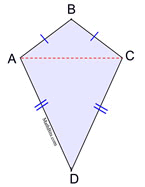 |
|
THEOREM: If a quadrilateral is a kite, it has one diagonal forming two congruent triangles.

|
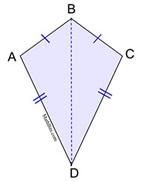 |
|
THEOREM: If a quadrilateral is a kite, it has one diagonal that bisects a pair of opposite angles.

|
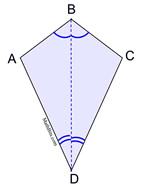 |
|
THEOREM: If a quadrilateral is a kite, it has one diagonal that bisects the other diagonal.

|
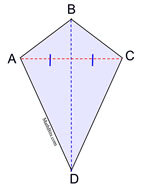 |
|
THEOREM: If one of the diagonals of a quadrilateral is the perpendicular bisector of the other, the quadrilateral is a kite.

|
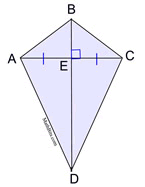 |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|