|
Note: The transformational statements on this page
are not formal proofs,
but are observations.
 |
Properties of parallelograms can
be observed through
symmetry. |
|
Definition: A parallelogram is a quadrilateral with
two sets of opposite sides parallel.
Definitions need no further observations, as they are stated facts.
A parallelogram has rotational symmetry when rotated
180º about its center.
A parallelogram has no reflectional symmetry.
|
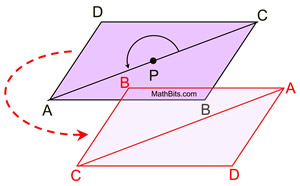
Rotational symmetry will map 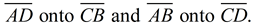
These sides coincide after the rotation,
so we can observe that AD = CB and AB = CD.
The opposite sides are congruent.
This rotation will also map ∠A onto ∠C
and ∠B onto ∠D, showing the
opposite angles congruent.
|
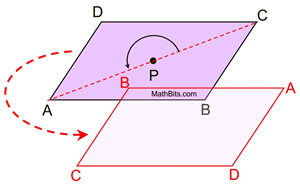 |
If we draw the diagonals, intersecting at P,
rotational symmetry will map
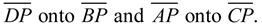
Theses segments will coincide after the rotation,
showing us that DP = BP and AP = CP,
which implies congruent segments.
Segment bisectors create congruent segments,
so we see the diagonals bisecting each other.
|
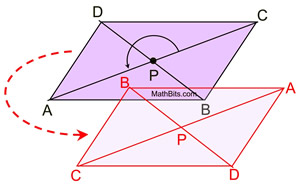 |
If we draw a single diagonal (either one),
we can observe that the rotational symmetry will
map ΔADC onto
ΔCBA.
This shows the diagonal creating two
congruent triangles.
|
 |
 |
Properties of rectangles can
be observed through
symmetry. |
|
Definition: A rectangle is a parallelogram
with four right angles.
A rectangle has reflectional symmetry when reflected over the line through the midpoints of its opposite sides.
Like the parallelogram, it also has rotational symmetry
of 180º about its center.
|
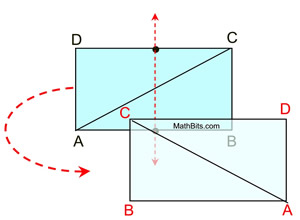
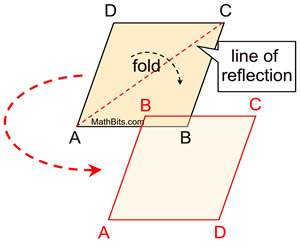
Reflectional symmetry,
(over the line of reflection shown),
will map
A onto B, and D onto C
(as well as B onto A and C onto D).
Since reflection is a rigid transformation,
we know that lengths are preserved.
|
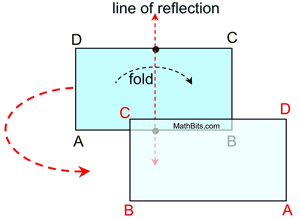 |
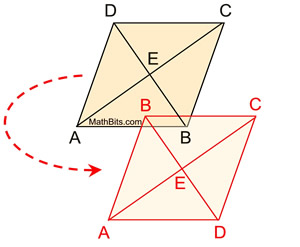
If we now draw the diagonal from A to C,
we know that the length of the diagonal will be preserved after the reflection.
Since the reflection maps
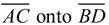 ,
we can see the diagonals congruent.
|
 |
 |
Properties of rhombus can
be observed through
symmetry. |
|
Definition: A rhombus is a parallelogram
with four congruent sides.
A rhombus has reflectional symmetry over either of its diagonals. |
 |
Like the parallelogram, it also has rotational symmetry of 180º about its center.
|
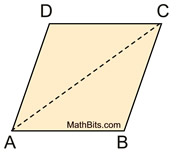
Reflectional symmetry,
over the diagonal from A to C,
will map D onto B, A onto A, and C onto C.
Since reflection is a rigid transformation,
we know that
angle measures are preserved.
m∠DAC = m ∠BAC and m∠DCA = m∠BCA,
showing that the angles are congruent.
The diagonal bisects the angles.
The same approach can be used with the diagonal from D to B.
|
 |
|
 |
 |
Properties of squares can
be observed through
symmetry. |
|
Definition: A square is a parallelogram
with four right angles and four congruent sides.
A square has reflectional symmetry when reflected over the line through the midpoints of its opposite sides, as well as over its diagonals. It also has rotational symmetry of 90º about its center.
|
Since a square is a parallelogram, a rectangle, and a rhombus, our symmetry observations for a square will be the same as those we have already seen. |
 |
A trapezoid has
no reflectional symmetry
and no rotational symmetry. |
|
Definition: A trapezoid is a quadrilateral with at least one pair of parallel sides.
We cannot make observations based upon symmetry.
|
 |
Properties of isosceles trapezoids
can be observed through
symmetry. |
|
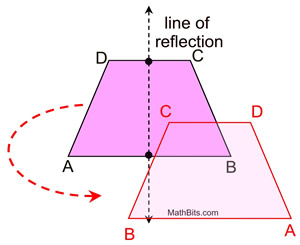
Definition: An isosceles trapezoid is a trapezoid with congruent base angles.
A isosceles trapezoid has reflectional symmetry when reflected over the line through the midpoints of its bases.
An isosceles trapezoid with only one pair of parallel sides has no rotational symmetry.
|
Reflectional symmetry,
(over the line of reflection shown),
will map A onto B, and D onto C
(as well as B onto A and C onto D).
Since reflection is a rigid transformation,
we know that lengths are preserved.
Leg 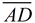 coincides with leg 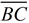 .
The legs are congruent.
During this reflection, which also preserves angle measure, ∠A will map onto ∠B and ∠D will map onto ∠C, making the base angles congruent.
|
 |
If we now draw the diagonal from A to C,
we know that the length of the diagonal will be preserved after the reflection.
Since the reflection maps
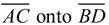 ,
we can see the diagonals congruent.
|
 |
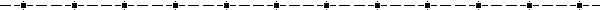
 |
Properties of kites
can be observed through
symmetry. |
|
Definition: A kite is a quadrilateral with two distinct pairs of adjacent sides congruent.
A kite has reflectional symmetry when reflected over its diagonal which connects the common endpoints of its congruent adjacent sides.
|
Reflectional symmetry,
(over the line of reflection shown),
will map A onto C, B onto B and D onto C
(as well as C onto A).
Since reflection is a rigid transformation,
we know that
angle measures are preserved.
∠A is mapped onto ∠C and m∠A = m∠C.
One pair of opposite ∠s congruent.
In addition, m∠ABD = m∠CBD and
m∠ADB = m∠CDB by the reflection preserving angle measure. Thus, the diagonal from B to D bisects ∠ABC and ∠ACD. One diagonal bisects the angles.
We can also observe that the reflectional symmetry will map ΔABD onto
ΔCBD.
Since length is preserved, this shows
this diagonal creating two
congruent triangles.
If we draw the second diagonal from A to C,
we can see that AE = CE by the mapping of 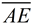 onto onto 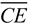 , with length being preserved. , with length being preserved.
One diagonal bisects the other.
Note: The diagonal DOING the bisecting is the diagonal which is also the line of reflection.
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|