|
|
An equation states that numerical, or algebraic, expressions are equal. Linear equations are equations of degree one, where the variable's exponent is one.
|
On this page, we will examine equations that require "two-steps" to solve. For a refresher, see Solving One-step Equations.
Linear equation: 2x + 8 = 18
Goal: Get the variable, x, ALONE on one side of the equal sign.
Remember to think of both expressions as "weighing" the same amount. You must be careful, when solving for the variable, to maintain an equal "weight" on both sides. This process of "balancing the equation" is accomplished by always making the same changes to BOTH sides of the equal sign.
|
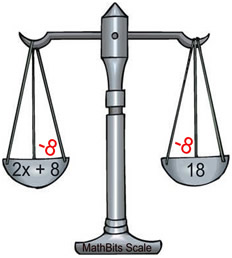 2x + 8 = 18 2x + 8 = 18
Subtract x from both sides. 2x = 10.
Divide both sides by 2. x = 5 |
|
 Solving two-step equations: Solving two-step equations:
Solve for x: 4x - 7 = 37 |
|
Analysis: More than one operation has been applied to the variable (4 has been multiplied and 7 has been subtracted ). We need to undo these operations in the correct order.
First, isolate the "term" containing the x. Get 4x by itself by adding 7 to both sides.
Next, undo the multiplication by 4, by dividing both sides by 4.
This 2-step process is (1) using the additive inverse property to create a 0 on the left side (-7 + 7 = 0), and using the additive identity to isolate the 4x, since 4x - 0 = 4x.
Then (2) the process is using the multiplicative inverse to create a value of 1 and the multiplicative identity to isolate x. |
|
 |
Undo any addition or subtraction first, then undo multiplication or division.
Just remember that we never divide by zero. |
|
Check answer: A nice bonus to solving equations is that you always know if you have the correct answer. Simply substitute your answer into the original equation and see if the result is true. |
Check:
4x - 7 = 37
4(11) - 7 = 37
37 = 37 True!
|

 Solving two-step equations with combining like terms on one side: Solving two-step equations with combining like terms on one side:
Solve for x: 3.4x + 8 - 9 = 16 |
|
Analysis: The left side of the equation contains two constant terms. Combine these "like" terms before beginning the solution of the equation.
First, combine 8 - 9.
Next, add +1 to both sides.
Then, divide both sides by 3.4.
Check:
3.4(5) + 8 - 9 = 16
17 + 8 - 9 = 16
16 = 16 True!
|
|
 Solving two-step equations with combining variables on one side: Solving two-step equations with combining variables on one side:
Solve for x: 2x + 8 + x = 35 |
|
Analysis: The left side of the equation contains two x terms. Combine these "like" terms before beginning the solution of the equation.
First, add 2x and x.
Next, subtract 8 from both sides.
Then, divide both sides by 2.
Check:
2(9) + 8 + 9 = 35
18 + 8 + 9 = 35
35 = 35
True! |
|
 Solving two-step equations with parentheses: Solving two-step equations with parentheses:
Solve for x: 3(2x + 5) = 63 |
|
Analysis: The left side of the equation contains parentheses. Distribute across the parenthesis before beginning the solution.
First, distribute 3 across the parentheses.
Next, subtract 15 from both sides.
Then, divide both sides by 6.
Check:
3(2(8) + 5)) = 63
3(16 + 5) = 63
3(21) = 63
63 = 63
True
|
|
 Solving two-step equations with decimals: Solving two-step equations with decimals:
Solve for x: 5x + 2.6 = 8.1 |
|
Analysis: Equations may contain decimals as constants (as seen here) or as coefficients.
There is no secret to solving problems with decimals. Simply solve as you would solve an equation with integer values.
Proceed as shown in the examples above.
|
|
Check answer: |
Check:
5x + 2.6 = 8.1
5(1.1) + 2.6 = 8.1
5.5 + 2.6 = 8.1
8.1 = 8.1 True!
|

 Solving two-step equations with fractions: Solving two-step equations with fractions:
Solve for x: 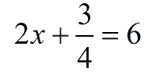 |
Method 1:
working with the fractions. |
Analysis: This equation contains a fraction. Remember that a fraction is a perfectly good number.
In solution Method 1, we will simply treat the fraction as a number and solve as we did in the previous examples.
Remember how division of fractions is working:
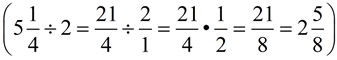
The correct answer could be written as an improper fraction, 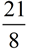 , or as a mixed number, , or as a mixed number, 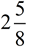 . The preferred method, however, is usually a mixed number. . The preferred method, however, is usually a mixed number.
|
|
Check answer: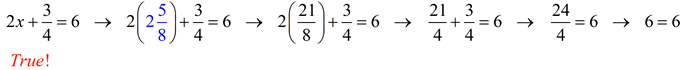
|
Solve for x: 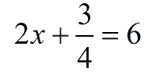 |
Method 2:
removing fractions. |
| Analysis: This equation contains a fraction. We want to remove the fraction from the problem.
In solution Method 2, we will remove the fraction.
It is possible to remove fractions from an equation before solving. Find the common denominator for all fractions within the equation, and then multiply EACH term by that value.
There is only one fraction in this example with a denominator of 4. So, we will multiply EACH term times 4 to create a new usable equation.
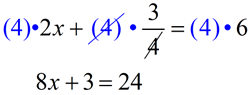 Now, solve this equation. Now, solve this equation. |
Multiply through by 4
to remove the fraction:
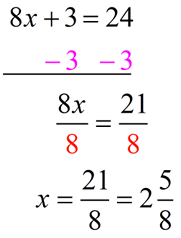 |
Check answer: [Always "check" back into the original equation, NOT the new equation.]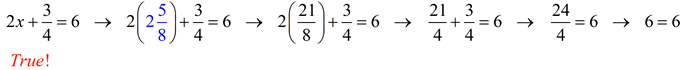 |
|
|
Yes, this example could also have been solved by changing 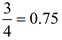 .
Changing fractions to decimals is a good solution method when the conversion gives a "nice" clean ending decimal, like 0.75, instead of a non-ending decimal such as 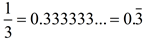 . |
|


NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|