|
For more introductory information see Solving Two Step Linear Inequalities.
|
The process for solving a linear inequality is the same as that for solving a linear equation, with one important exception ... |
|
... when you multiply (or divide) an inequality by a negative value,
you must change the direction of the inequality. |
|

Solve and graph the solution set of: 5(x - 3) > 10 |
Proceed as you would to solve a linear equation.
Distribute (remove the parentheses).
Add 15 to both sides.
Divide both sides by 5.
Note: The direction of the inequality stays the same since we did NOT multiply by a negative value.
Graph using a open circle for 5 (since x can NOT equal 5) and an arrow to the right (since our symbol is greater than). |
|

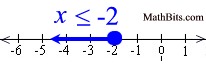
Solve and graph the solution set of: 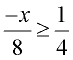 |
Multiply both sides by the least common denominator, which is 8.
Divide both sides by -1, and flip the direction of the inequality.
Note: The direction of the inequality was reversed since we divided by a negative value (-1).
Graph using a closed circle for -2 (since x can equal -2) and an arrow to the left (since our symbol is less than or equal to). |
|
Solve and graph the solution set of: 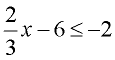 |
Add 6 to both sides.
Multiply both sides by 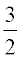 .
Note: The direction of the inequality stays the same since we did NOT multiply by a negative value.
Graph using a closed circle for 6 (since x can equal 6) and an arrow to the left (since our symbol is less than or equal to).
|

|

Solve and graph the solution set of: 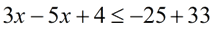 |
Combine the x-values on the left side.
Combine the numeric values on the right.
Subtract 4 from both sides.
Divide both sides by -2.
Note: The direction of the inequality was reversed since we divided by a negative value.
Graph using a closed circle for -2 (since x can equal -2).
|
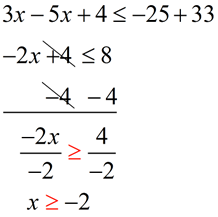
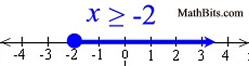
|

Solve and graph the solution set of: 5 - 2 x 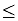 13 + 2 x |
Add 2x to both sides.
Subtract 13 from both sides.
Divide both sides by 4.
Note: There was no multiplication or division by a negative value, so the inequality symbol did not get reversed.
Graph using a closed circle for -2 (since x can equal -2).
|
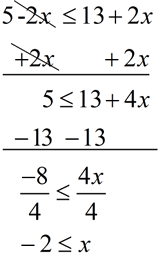
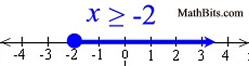
|
Solve and graph the solution set of: 4x + 10 < 3(2x + 4) |
Distribute across parentheses.
Subtract 4x from both sides.
Add -12 to both sides.
Divide both sides by 2.
Note: There was no multiplication or division by a negative value, so the inequality symbol did not get reversed.
Graph using a closed circle for -2 (since x can equal -2).
|
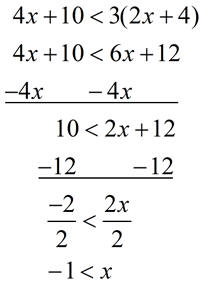

|
 
Solve and graph the solution set of: 2(3x - 1) > 6x - 5 |
 Dealing with ALL Answers TRUE: Dealing with ALL Answers TRUE:
If the variable cancels out when solved, and you are left with a TRUE numerical statement, the solution will be ALL REAL NUMBERS work. |
Distribute across the parentheses.
Subtract 6 x from both sides.
Notice the TRUE numerical result.
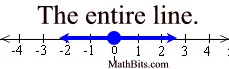
The solution to this inequality is the entire set (all) Real Numbers.
The graph is the entire number line. |
2(3x - 1) > 6x - 5
6x - 2 > 6x - 5
-6x -6x
-2 > -5 TRUE
Think of the positions of -2 and -5
on a number line.
This tells us that any x-value that is a Real Number will make this inequality true.
Solution: ALL REAL NUMBERS
|
 
Solve and graph the solution set of: 4(2x + 1) < 8x + 4 |
Distribute across the parentheses.
Subtract 8x from both sides.
Notice the FALSE result.
The solution to this inequality is the "empty set" (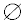 ). There are no x-values which will make this inequality true. ). There are no x-values which will make this inequality true.
There is nothing to be graphed. |
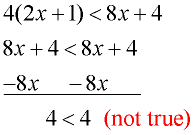 This tells us that NO x-values will make this inequality true.
This tells us that NO x-values will make this inequality true. 
|
| In this problem, the left side of the inequality is simply another way of writing the right side of the inequality. The two sides are EQUAL to one another. Since a quantity can never be less than itself, this inequality is never true. |
|
|
Yes, there is a way to determine solutions for inequalities on your graphing calculator. Click the calculator at the right to see how to use the calculator with single variable inequalities.
|
|
|
|
For calculator help with inequalities
(single variable)
click here. |
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|