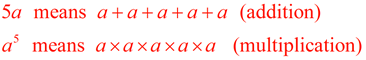The discovery of exponents gave us the capability to communicate certain mathematical concepts in a much faster and more efficient manner. You have seen the use of exponents as they applied to powers of 10.
Now, let' take a look at exponents as they are applied to whole numbers in general.
The exponent of a number indicates how many times to use
that number under multiplication.
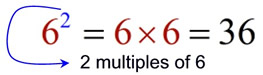
In this example, 6 is called the "base" and 2 is called the "exponent".
Exponential Notation |
Expanded Notation |
Standard Notation |
|
|
|
The word "exponent" is often synonymous with the word "power".
62 can be read as "6 raised to a power of 2" or "6 squared".
43 can be read as "4 raised to a power of 3" or "4 cubed".
The base value is a number being used as a "repeated factor".
|


|
The use of an exponent is referred to as repeated multiplication. 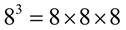
Remember that multiplication is referred to as repeated addition . 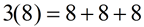
Important Concepts:
|
| |
• 43 = 4 × 4 × 4 (the 4 is being used as a repeated factor)
• 127 = 12 × 12 × 12 × 12 × 12 × 12 × 12
127 is in "exponential form"
12 × 12 × 12 × 12 × 12 × 12 × 12 is in "expanded form"
• 81 = 8 (any number raised to a power of 1 is equal to itself)
• 60 = 1 (any number raised to a power of 0 is one, but 00 is undefined)
• 53 = 5^3 (this is an alternate notation often seen on computers and calculators)
• 105
= 10 × 10 × 10 × 10 × 10 = 100,000 (remember when working with powers of 10,
the exponent becomes the number of zeros in the standard notation)
• 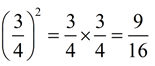 (the base value can be a fraction, or even a decimal) (the base value can be a fraction, or even a decimal)
• 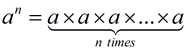 (n multiples of the value of a) (n multiples of the value of a) |

Exponents and Units of Measure:
When working with units of measure and exponents (or powers),
remember to adjust the units appropriately:
(25 in)3 |
= (25 in) • (25 in) • (25 in)
= (25 • 25 • 25 )(in • in • in)
= 15625 in3 |


1. Write this expression in expanded form and then evaluate: (5.2)3
(5.2)3 = 5.2 x 5.2 x 5.2 = 140.608
2. Write this expression in exponential form and then evaluate: 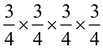
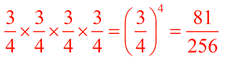
3. Write seven cubed in exponential, expanded, and standard forms,

4. Explain the difference between 5a and a5.