|
• First, understand that the "error" is always considered to be positive concept.
• Now, to find the error, subtract one value from the other. The order of the subtraction is not important.
Example: John measured a flexible covering to be 38 inches, when it was actually 40 inches.
By subtraction, we have 40 - 38 = 2, the error.
Or we can have, 38 - 40 = -2, (ignore negative sign), so 2 is the error. |
Find the Percent of Error: |
• Express the error as a percent of the "exact" value.
Divide the error by the exact value and express as a percent.
(The "exact value" may also be called the "known value".)
|
|
As a formula, we have:
Notice that the |measured value - known value| is the subtraction which created the error. The absolute value of the subtraction guarantees the error is expressed as a positive value.
Example: John measured a flexible covering to be 38 inches, when it was actually 40 inches.
By subtraction, we know that the error is 2.
The percent of error will be 2/40 = 0.05 = 5%.
Divide by the known (exact) value. |
If we use the formula, we have:
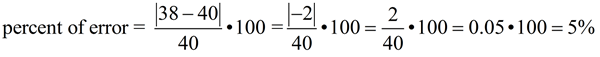

Percent of Error vs Percent of Change: |
We have seen problems that determine the "percent of increase" or the "percent of decrease" between two quantities. At first glance, it may appear that "percent of error" is the same process. Yes, the strategies are similar, but there is a difference.
"Percent of increase" and "percent of decrease" can be referred to as "percent of change".
Both of these situations, are based on the fact that a "change" has occurred. Thus, there was a "before" the change value, and an "after" the change value.
When the "after" value is greater than the "before" value, you have a percent of increase problem. Otherwise, it is a percent of decrease situation. The amount of the change will always be positive. If there is a negative sign, it simply implies decrease instead of increase.
To find the change: subtract the "before" value from the "after" value to get the change.
To find the percent of change: divide the "change" by the "before" value and convert to a percent.
As a formula, we have:
So what is the difference between percent of error and percent of change?
Percent of change (or "Percent of increase" or "percent of decrease") is based upon what happened first.
Percent of error is based upon the actual known to be true value. It doesn't care about what happened first.
EXAMPLE:
John guessed that there would be 20 people at the skating rink, but actually 32 people showed up.
a) What was
John's percent of error on his guess?
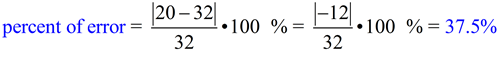
b) What was John's percent of change (percent of increase) between his prediction and the actual number of people?
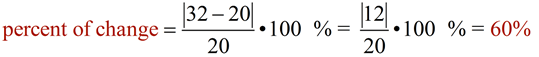
In this example, you can see that the "percent of error" did not care that John's guess came "before" he knew the actual number of people at the skating rink. Percent of error always divides by the known (exact) value.

Percent of Error:
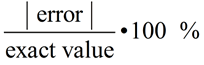 subtract / known value
subtract / known value
|
|
Percent of Change:
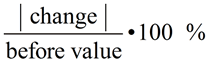 subtract / before value
subtract / before value
|
|
The percent of error compares the guess to the exact value. |