More work with percents and money.
We will be looking at the word commission as it pertains to a percentage of an amount of items sold. There are certain sales-based occupations where people are paid a commission. It may be that a person works on commission only, or that a person earns a base salary (guaranteed salary) plus a commission.
| 1. Bugs is paid by commission only. He is paid 15% of every carrot juicer he sells. If Bugs sells $120 worth of juicers in one week, what is his salary for that week? |
Solution: 15% of $120 = 0.15 x 120 = 18
Bugs earns $18 for that week. |
|
| 2. Angela earns a monthly base salary of $4,000. It is expected that she will sell $16,000 worth of items each month (called a "quota"). She will receive a 12% commission on all sales beyond her monthly quota. If Angela sells $22,180 for the month of September, what is her total monthly salary for September? |
Solution: The amount sold OVER the quota is $22180 - $16000 = $6180.
$4000 + 12% of ($6180) = $4000 + 0.12 x 6180 = 4741.60 Angela earns $4,741.60 for Sept.

The term fee refers to a payment made to a professional, an agency, an organization, a public body, etc. in return for services. Fees are often expressed in terms of a percent.
3. Aisha wants to sell her skateboard for $45 on the Sell-It web site, which sells items for individuals. Sell-It will sell her skateboard, collect the money and deposit the money in Aisha's account. Sell-It will deduct a fee of 8.2% of the sale price.
What will be the final amount of money Aisha receives for her skateboard? |
Solution:
First find the amount of the fee: (this is a "% of " problem) $45 x 8.2% = 45 x 0.082 = $3.69 fee
Now, subtract the fee from Aisha's selling price: $45 - $3.69 = $41.31 Aisha's final amount
 |
 A problem, such as the example above, where the answer requires finding the fee and then subtracting the fee from the original selling price, is referred to as a two-step process. A problem, such as the example above, where the answer requires finding the fee and then subtracting the fee from the original selling price, is referred to as a two-step process.
Step 1: The percentage of the price, the fee, is found.
Step 2: The fee is subtracted from the original selling price.
|
It may be possible, in these types of problems, to combine the two steps into one-step.
Charging a fee of 8.2% means 8.2% of the her money is taken away.
Then what is left (100% - 8.2%), or 91.8%, remains.
Rather than find 8.2% and then subtract, simply find 91.8% of the money to start.
Money Aisha receives: 91.8% of $45 = 0.91.8 x 45 = $41.31
|

Everyone is familiar with checking accounts and savings accounts.
What you put into these accounts is called a deposit.
What you take out of these accounts is called a withdrawal.
The amount of money in an account is called the balance.
| 4. Courtney has $356 in her checking account. Over the course of a week, she writes checks for $45.95, $12.50, and $75.86 and makes a deposit of $35.00. What is the balance of her checking account at the end of this week? |
Solution: $356.00 - $45.95 - $12.50 - $75.86 + $35.00 =
$256.69
|
 Regarding the withdrawals in this problem: you could add all of the withdrawals together first and then subtract that one amount.
Regarding the withdrawals in this problem: you could add all of the withdrawals together first and then subtract that one amount. |

The word interest refers to a percentage of money that is "borrowed".
It is a common practice to "borrow" money, in the form of a loan, from the bank to purchase expensive items. The borrower slowly re-pays the money back to the bank plus an interest charge for the privilege of "borrowing" the money.
In regards to "saving" money, people often get creative and hide their money in the closet, or bury it in the backyard. But for safety reasons (the dog might dig up the backyard stash) and to earn money on the amount being saved, most people deposit their money into a savings account at their local bank. In this situation, the bank pays the interest to the account holder. The bank pays the individual for the privilege of "borrowing" his/her money (to be used in investments to make money for the bank).
We will be working with a type of interest called "simple interest", which is the interest computed on the original amount borrowed or deposited.
Interest, I, is the amount charged or earned.
Interest Rate, r, is the percent used to determine the interest charged or earned.
Principal, P, is the original amount deposited or borrowed.
Time, t, is the specific time period, such as years, months, or days (usually expressed in years).
|
Simple Interest Formula:
I = P • r • t
I = interest
P = principal
r = rate (decimal)
t = time (years) |
There are other types of "interest" problems and formulas
which will be studied in future courses. |
| |
| 5. Alex borrows $5000 at an annual simple interest rate of 8% for one year. What is the interest that will be owed for one year? |
Solution: 8% of $5000 = 0.08 x 5000 = 400. The interest owed will be $400.
If Alex wanted to pay off this loan in one year, he would owe $5000 + $400, for a total of $5,400.
Using the Simple Interest Formula: I = 5000 x 0.08 x 1 = $400.
| 6. Ari opens a savings account that pays simple interest at the rate of 4½% per year. If he deposits $3000 and makes no other deposits or withdrawals, find the interest and the final amount for a period of 90 days. |
Solution: Since the interest rate is in "years" but the problem is dealing with "days", we need to represent the time as a fractional part of a year by dividing the number of days by 365.
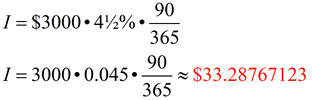
Since money is always rounded to the nearest penny (nearest cent), the interest is $33.29.
The final amount for 90 days is $3000 + $33.29 = $3033.29.
|