Things to remember about percents:
A percent is a fraction with a denominator of 100.
5% means "5 for each 100" or 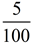 |
|
A percent can always be written as a decimal, and vice versa.
Change a decimal to a percent:
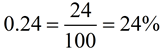 Move the decimal two places to the right to create the percent.
Move the decimal two places to the right to create the percent.
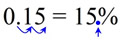
|
|
Change a percent to a decimal:
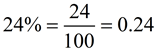 If there is no decimal showing in the percent, it will be behind the number. Move the decimal two places to the left to change to a decimal value.
If there is no decimal showing in the percent, it will be behind the number. Move the decimal two places to the left to change to a decimal value.
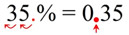
|
|
Fractional Equivalents:
Percent
|
1% |
10% |
25% |
|
50% |
|
75% |
100% |
| Fraction |
|
|
|
|
|
|
|
|
Knowing fraction equivalents for some percents may make computations easier and faster.
25% of 12 = ¼ of 12 = 3
Remember, percents refer to "out of 100" or "part of 100".
Think of fractions with a denominator of 100.
A percent of a quantity can be seen as a rate per 100.
(25% of a quantity means 25/100 times the quantity) |
|
The word "percent" is from the Latin "per centum" meaning
"per hundred". |
|
When working with percents, you may be asked to find different components of a problem.
There are three main types of problems dealing with percents:
1. finding a percent of a number.
In this type of problem, it will be necessary to change the percent to a decimal value (or a fraction), and multiply.
 Find 8% of 340. Find 8% of 340.
Solution:
Let x = the answer
x = 8% • 340 (of means to multiply)
x = 0.08 • 340 (change to a decimal)
x = 27.2 |
Remember that the word "of " means to multiply! |
|
|
2. finding a number when a percent of that number is known.
In this type of problem, it will be necessary to set up an equation to represent the problem.
Solving the equation will yield the answer.
 45 is 30% of what number? 45 is 30% of what number?
Solution:
Let n = the number wanted
Write the problem literally as you see it:
45 = 30% • n (set up an equation)
45 = 0.30 • n (change 30% to decimal)
45/0.30 = n (divide both sides by 0.30)
n = 150 |
Set up an equation.
Remember that the word "is" means equal
and the word
"of " means multiply! |
|
|
3. finding what percent one number is of another.
In this type of problem, we will look at two types of solutions. First is a method that uses an equation with the % written as a fraction. Second is a method that uses the % written as a fraction and a proportion.
 6 is what percent of 24? 6 is what percent of 24?
Solution using first method:
In this method, it will be necessary to represent the percent as a fraction with a denominator of 100, and set up an equation to represent the problem. Solving the equation will yield the answer.
|
Let x = the percent
Write the problem literally as you see it:
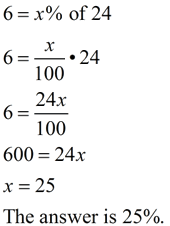
|
Remember to change a percent to a fraction, divide the percent value by 100. |
Set up an equation.
The word "is" means equal,
the % becomes a fraction,
and the word
"of " means multiply!
|
|
|
 6 is what percent of 24? 6 is what percent of 24?
Solution using second method:
In this method, use the proportion setups shown at the right. For this problem, 6 will be the "part" and 24 will be the "whole".
Let x = the percent
Write the proportion as directed above: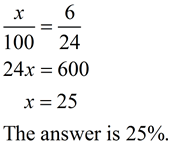
|
When using "IS over OF",
IS represents the "part" and
OF represents the "whole". |
Notice that "part over whole" is the definition of a fraction. |
|
Remember, in a proportion you can use "cross multiply"
(or "cross product").
(Actual Statement:) In a proportion, the product of the means equals
the product of the extremes. |
|
|
|