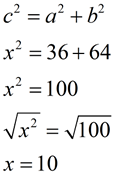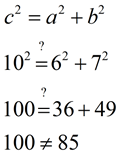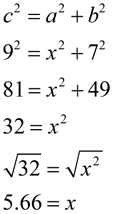|
One of the most well-known geometric concepts is that of the Pythagorean Theorem.
While the Babylonians understood the relationship regarding the sides of a right triangle nearly 1,000 years before Pythagoras, it was Pythagoras that first "proved" the concept. Pythagoras popularized the relationship between the hypotenuse and the legs of a right triangle, and discovered that this relationship is true for ALL right triangles. As the first mathematician to geometrically prove this theorem, the theorem bears his name.
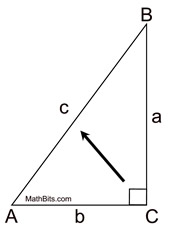
Pythagorean Theorem: In any right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs. |
|
 Pythagoras
Pythagoras 500 BC
Greek Mathematician |
Pythagorean Theorem
c2 = a2 + b2
for any right triangle
a and b are "legs"
c is the "hypotenuse"
(c is across from the right angle)
(leg a)² + (leg b)² = (hypotenuse c)²
|
|
|
The Pythagorean Theorem ONLY works in Right Triangles. |

There are certain sets of numbers (positive integer values) that have a very special property in relation to the Pythagorean Theorem. Not only do these numbers satisfy the Pythagorean Theorem, but any multiples of these numbers also satisfy the Pythagorean Theorem.
For example: the numbers 3, 4, and 5 satisfy the Pythagorean Theorem: 32 + 42 = 52.
If you multiply all of these numbers by 2 (6, 8, and 10), these new numbers ALSO satisfy the Pythagorean Theorem:
62 + 82 = 102.
The special set of numbers that possess this property are called
Pythagorean Triples. |
Three of the most common Pythagorean Triples are:
3, 4, 5 |
5, 12, 13 |
8, 15,17 |

Converse of the Pythagorean Theorem: |
If we write the Pythagorean Theorem in "if - then" form we have:
 Pythagorean Theorem: If a triangle is a right triangle, then the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the lengths of the legs (the other two sides). Pythagorean Theorem: If a triangle is a right triangle, then the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the lengths of the legs (the other two sides). |
Now, if we reverse the "if" and "then" portions of the Pythagorean Theorem, we will get the "converse" of the Pythagorean Theorem.
 CONVERSE of Pythagorean Theorem: If the square of the length of the longest side of a triangle is equal to the sum of the squares of the lengths of the other two sides, then the triangle is a right triangle. CONVERSE of Pythagorean Theorem: If the square of the length of the longest side of a triangle is equal to the sum of the squares of the lengths of the other two sides, then the triangle is a right triangle. |
This converse theorem is used to prove that a triangle is a right triangle.
If you plug numbers into the Pythagorean Theorem and the numbers make the Theorem true, the numbers are the sides of a right triangle.

The Pythagorean Spiral (also called the Square Root Spiral or the Spiral of Theodorus) is shown at the right.
The spiral is a series of right triangles, starting with an isosceles right triangle with legs of length one unit. Another right triangle is built upon the first triangle with one leg being the hypotenuse from the previous triangle and the other leg having a length of one unit. This process is then repeated.
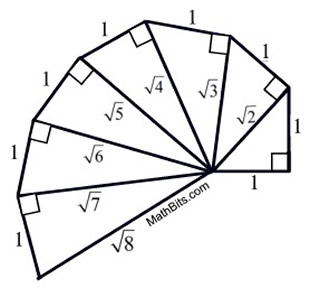
Most diagrams of the spiral stop with the hypotenuse being 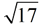 , as the next right triangle will overlap the starting triangle. , as the next right triangle will overlap the starting triangle. |
 |
The spiral can be extended beyond the hypotenuse of 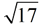 and the triangles will begin to overlap previous triangles. In 1958, Erich Teuffel proved that while the triangles may overlap, no two hypotenuses will ever coincide, no matter how far the spiral is continued. |


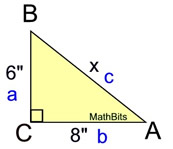
Find x.
Answer: 10"
|
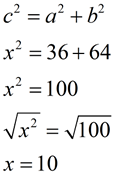 |
|


A triangle has sides 6, 7, and 10. Is it a right triangle?
Let a = 6, b = 7 and c = 10. The longest side MUST be the hypotenuse, so c = 10.
Substitute into the Pythagorean Theorem to see if it is TRUE. This will be using the Converse of the Pythagorean Theorem.
|
Since the Pythagorean Theorem is NOT true, these sides can NOT
be the sides of a right triangle.
|
These sides could, however, be the sides of a non-right triangle,
since the sides satisfy the Triangle Inequality Theorem where
the sum of any two sides is > the third side.


A ramp was constructed to load a truck. If the ramp is 9 feet long and the horizontal distance from the bottom of the ramp to the truck is 7 feet, what is the vertical height of the ramp to the nearest tenth of a foot?
Since the ramp is described as having horizontal and vertical measurements, a right angle is implied. Solve using the Pythagorean Theorem.

Find x.
Answer: 5.7 feet
|
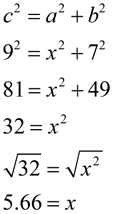 |
The height of the ramp is 5.7 feet. The ramp will allow packages to be loaded into an area of the truck that is too high to be reached from the ground. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|