|
|
When multiplying polynomials, each term from one polynomial must be multiplied by each term of the other polynomial. |
Since each term in a polynomial is a monomial, multiplying polynomials becomes multiplying monomials.
 Multiply a Monomial by a Monomial: Multiply a Monomial by a Monomial:
|
When multiplying monomials, use the product rule for exponents. 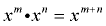 |
|
|
The factors are regrouped, and then multiplied. Notice the product rule for exponents at work [when the bases are the same, add the exponents]. |
|
|
Be careful of the signs associated with each term. |
|
|
If more than one variable is involved, group each variable separately. |
As with all mathematical procedures, as you become more confident in your skills, you may be able to process some of these steps mentally. |
 Multiply a Monomial by a Polynomial: Multiply a Monomial by a Polynomial:
|
When multiplying a monomial by a polynomial, use the distributive property.
|
The traditional statement of the distributive property shows a monomial times a binomial:
a • (b + c) = a • b + a • c
This statement can be expanded when more terms are involved:
a • (b + c + d + ... + n) = ab + ac + ad + ... + an.
|
|
|
(monomial x binomial)
The 3x2 is distributed (multiplied) by each term in the binomial. The process then becomes multiplying a monomial times another monomial. |
|
|
(monomial x trinomial)
Be careful to distribute the 0.2x times all three terms in the trinomial. Watch out for those decimal points! |
|
|
(monomial x polynomial)
Be sure to distribute -4a3 times all four terms. Be careful of the signs. Don't forget the negative sign in -4a3. |
 Monomial Multiplication with Algebra Tiles: Monomial Multiplication with Algebra Tiles:
This set up of Algebra tiles gives you a "visual" demonstration of multiplying monomial x times binomial (x + 3).
Key: 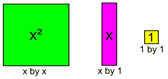
See more about Algebra Tiles. |
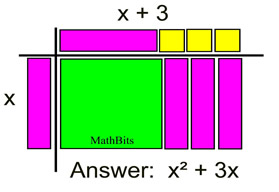 |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|