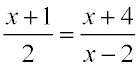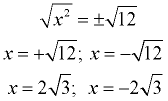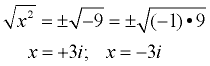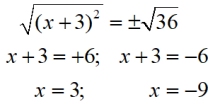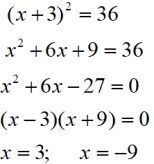|
We will be examining 5 strategies for solving quadratic equations.
This lesson covers the first two of our listed strategies.
Standard form of a quadratic equation: ax2 + bx + c = 0.
Degree of 2: The most number of solutions will be 2.
The most number of times the function will cross the x-axis will be 2.
While we will discover that quadratic equations can have 0, 1 or 2 solutions (roots),
the majority of the equations we will be examining will have 2 solutions. |

 As you examine these methods of solving quadratic equations, notice the relationship between the answers (roots, zeros) and the graphs of the quadratic equations. (equation's roots => graph's x-intercepts, called zeros) As you examine these methods of solving quadratic equations, notice the relationship between the answers (roots, zeros) and the graphs of the quadratic equations. (equation's roots => graph's x-intercepts, called zeros) |
 To solve a quadratic equation by factoring: To solve a quadratic equation by factoring:
For more details on the process of factoring, see the Factoring section.
The information presented on this page is meant as a refresher of those factoring skills, as they pertain to quadratic equations.
| |
Factoring Method |
1. |
Express the equation in the form ax2 + bx + c = 0. |
2. |
Factor the left hand side (if 0 is on the right). |
3. |
Set each of the two factors equal to zero. |
4. |
Solve for x to determine the roots (or function's zeros). |
|
Simple quadratic equations with rational roots can be solved by factoring. Let's refresh our memories on factoring these simple quadratic equations as they appear in different situations.
Refer to Factoring for more examples.
|
Examples of Solving Quadratic Equations by Factoring:
Factoring with GCF
(greatest common factor):
|
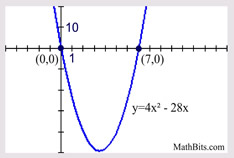
Solve: 4x2 - 28x = 0
4x(x - 7) = 0
4x = 0; x - 7 = 0
x = 0; x = 7
|
|
Find the largest value which can be factored from each term on the left side of the quadratic equation.
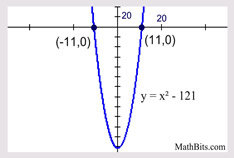
The roots correspond to the locations of the x-intercepts (zeros) of the function
y = 4x2 - 28x. |
Factoring Trinomial with Leading Coefficient of One:
|
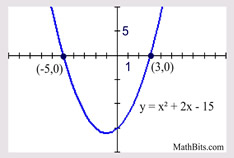
Solve: x2 + 2x - 15 = 0
(x + 5)(x - 3) = 0
x + 5 = 0; x - 3 = 0
x = -5; x = 3
|
|
When the leading coefficient is one, the product of the roots will be the constant term, and the sum of the roots will be the coefficient of the middle x-term. |
Factoring Difference of Two Squares:
|
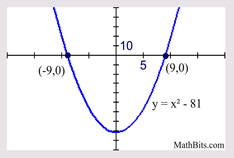
Solve: x2 - 81 = 0
(x + 9)(x - 9) = 0
x + 9 = 0; x - 9 = 0
x = -9; x = 9
|
|
Remember the pattern for the difference of two squares, where the factors are identical except for the sign between the terms.
|
Factoring Trinomial with Leading Coefficient Not One:
|
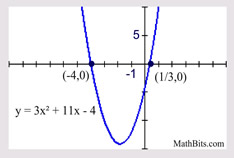
Solve: 3x2 + 11x - 4 = 0
(3x - 1)(x + 4) = 0
3x - 1 = 0; x + 4 = 0
x = 1/3; x = -4
|
|
Life gets more difficult when the leading coefficient is not one. Check out the Factoring section to see more strategies for factoring these pesky problems. |
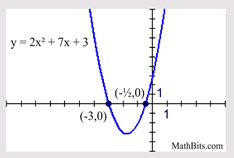
Where's the x2 ?
|
Solve: 2x(x + 4) = x - 3
2x2 + 8x = x - 3
2x2 + 7x + 3 = 0
(2x + 1)(x + 3) = 0
2x + 1 = 0; x + 3 = 0
x = - 1/2; x = -3
|
|
Sometimes you have to "work" on the equation to get the needed quadratic form. In this case, distribute, and the x2 will appear. |
Dealing with Proportions: |
Solve: 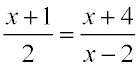
2( x + 4) = ( x + 1)( x - 2)
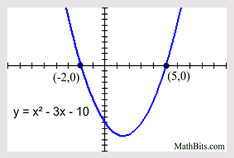
2 x + 8 = x2 - x - 2
0 = x2 - 3 x - 10
0 = ( x - 5)( x + 2)
x - 5 = 0; x + 2 = 0
x = 5; x = -2
|
|
x2 may appear when cross multiplying ("product of the means equals product of the extremes") is employed in a proportion. |
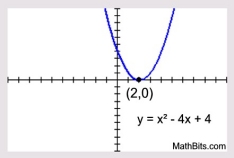
Repeated Root: |
Solve: x2 - 4x + 4 = 0
(x - 2)(x - 2) = 0
x - 2 = 0; x - 2 = 0
x = 2; x = 2
Repeated Root
|
|
Notice that x2 - 4x + 4 = (x - 2)2 or (x - 2)(x - 2). The factor repeats, so the solution (root) repeats, giving only ONE solution.
The function only intersects the x-axis once, being tangent at (2,0). |

Dealing with Equations such as: y = ax2
| |
Square
Root Method (ax2 is the only variable term) |
1. |
Isolate the ax2 term on one side of the equation. |
2. |
Take the square root of both sides. |
3. |
Remember to use ±, as there are two solutions. |
4. |
Express the roots (or zeros of the function). |
|
You have seen this method before.
The square root method applies only to one specific situation. This method works when there is no middle bx term in the equation. The only variable in the equation is an x2 term.
|
Examples of Solving Quadratic Equations by Square Root Method:
Easiest Set-Up (has "x2 = __"): |
Solve: x2 = 121
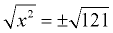
x = ±11
|
|
This is a simple, straight forward example. In this example, the constant is a perfect square. |
Difference of Two Squares:
|
Solve: x2 - 81 = 0
x2 = 81
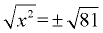
x = ± 9
|
|
We saw this example under the "factoring method" in the section above. Here it is again, being solved by the "square root method". Of course, the answers are the same.
|
Only variable is the x2 term, with subtraction of constant. |
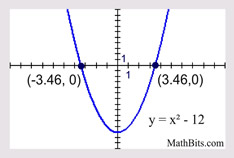
Solve: x2 - 12 = 0
x2 = 12
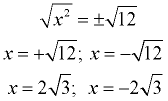
Approximate decimal answers:
x = -3.464102 and
x = 3.4641016 |
|
This example shows the numeric value (the constant), subtracted from the x2 term. Isolate the x2 term. Take the square root of both sides. |
FYI: Only variable is the x2 term, with addition of constant. |
Solve: x2 + 9 = 0
x2 = -9
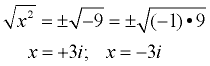
This problem has no real number solutions.
|
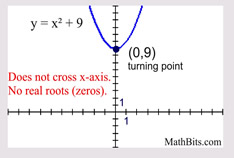 For study in future courses.
For study in future courses. |
This example shows the numeric value (the constant), added to the x2 term. This creates a problem with a negative value under the square root. In future courses, we will deal with this problem which creates "complex" answers containing the imaginary "i". |
Sneaky situation:
Dealing with a parentheses squared (a binomial squared). The x2 term will look like
(x + a)2. |
Solve: (x + 3)2 = 36
Hint: do NOT expand
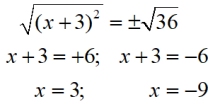
|
If you expand the parentheses, the problem becomes a "factoring" problem.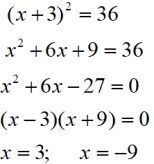 |
The sneaky part to this problem is to NOT expand the parentheses. Treat the parentheses as a value being squared and take the square root of that squared value.
Of course, you "can" expand, but the square root approach is faster.
|
This last "sneaky situation"
strategy will be very important in the next lesson.
Be sure you understand what is happening in this method.

There are tools more powerful than "factoring" and "square root method"
for solving quadratic equations.
Check out these other strategies for solving quadratic equations:
completing the square and quadratic formula. |
|
For calculator help with graphing parabolas
click here. |
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|