You may, or may not, have seen "inverse functions" in Algebra 1.
If you have not, don't worry. We will start with an introduction in this unit. |
You have seen the concept of "inverse" in Algebra1. For example, you know that squaring and square rooting are "inverse" operations. One operation "undoes" the other operation.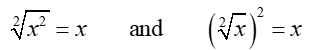
Taking the square root of x2 equals x.
Taking the square of the square root of x = x.
This same concept of "inverse" can be applied to functions.
It is of special importance when working with exponential functions.
We will start with a basic introduction into inverse functions in this unit,
with more details developed in the unit Function Concepts.
 inverse notation
 |
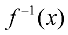The inverse of a function is the set of ordered pairs obtained by interchanging the first and second elements of each pair in the original function.
In other words, one function "undoes" what the other function did. |
|
In plain English, finding an inverse is simply the swapping of the x and y coordinates.
f (x) = {(2,3), (4,5), (-2,6), (1,-5)} (function)
The inverse of f (x), written as f -1(x), = {(3,2), (5,4), (6,-2), (-5,1)} (function)
Let's look at another example: g (x) = {(4,1), (8,3), (-5,3), (0,1)} (function)
The inverse of g (x). or g-1(x),= {(1,4), (3,8), (3,-5), (1,0)} (NOT a function, the x = 3 repeats.)
 The inverse of a function may NOT always be another function!
Only functions that are one-to-one functions have inverses that are also functions.
A function is a one-to-one function if each value in the range
corresponds
with exactly one value in the domain. No y-values get used more than once.
This fact of possible non-function results leads to some subtle differences in terminologies:
Definition: The Inverse of a Function is the "relation" formed when the independent variable (x) is exchanged with the dependent variable (y) from a given function. (This inverse may NOT be a function.)
Definition: An Inverse Function is when the result described above is also a "function". The result is then called an inverse function. |
Inverses: Getting back to where you started!
( and composition of functions)
|
|
During our work with inverses, as they relate to exponential and logarithmic functions, we need to have a basic understanding of a process called "composition of functions".
You actually started working with this concept of "putting functions together" back in Algebra 1.
Consider this Algebra 1 problem: Given f (x) = 2x2 + 4x + 3, find f (2x+ 3).
The solution is to substitute "2x + 3" for "x" in the "definition" of f (x), and simplify.
f (2x + 3) = 8x2 + 32x + 27.
This problem illustrates the basic concept of composition of functions.
If we use "2x + 3" to define g(x), we can now write f (2x + 3) = f (g(x)) by substitution.
f (g(x)) is seen as a composition of 2 functions and the result from g(x)
becomes the input for f (x).
f (g(x)) = f (2x + 3) = 8x2 + 32x + 27.
Read more at Composition of Functions. |
The functions f (x) and g(x) in the example above are not
"inverses" of one another.
If they had been inverses, then the composition would have a specific outcome.
Remember what happens with a function and its inverse:
f (x) = {(2,3), (4,5), (-2,6), (1,-5)}
f -1(x) = {(3,2), (5,4), (6,-2), (-5,1)}
The inverse of the function takes the output from the given function,
performs some operation on it, and arrives back at the original function's starting input value,
the original x-coordinate.
A function and its inverse "undo" one another, leaving you right back where you started.
The idea of "back where you started" is actually the formation of the Identity Function, y = x.
Composition of functions (or composite function):
f (f -1(x)) = x or in reverse: f -1(f (x)) = x
These output values of x form the Identity Function line, y = x,
over which a function and its inverse are reflected.
.
So how do we find these inverse relationships?
 Method 1 (tables and ordered pairs):
If the function is stated as a set of ordered pairs, we can find the inverse of the function by simply swapping the ordered pairs (as was shown at the top of this page).
If the equation of the function is fairly simple, we may be able to find the equation of the inverse of the function by examining the ordered pairs listed for the inverse.
Let f (x) = x + 1
x |
y=f (x) |
1 |
2 |
3 |
4 |
-2 |
-1 |
0 |
1 |
|
Inverse of f (x)
x |
y=f -1(x)
|
2 |
1 |
4 |
3 |
-1 |
-2 |
1 |
0 |
|
It can be seen from this example that the inverse will be subtracting one from each of its input values.
Inverse of f (x) = x + 1,
or
|
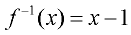
NOTATION:
An inverse function is denoted by
.
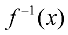(as it did in relation to exponents)
|
|
You can see how the second table above "undoes" the results from the first table,
and returns to the original list of starting x-values from the first table.
Method 2 (algebraic equations):
There is a simple method to find the inverse of the equation of a function algebraically.
Process
1. Set the function = y
2. Swap the x and y variables
3. Solve for y. |
|
Find the inverse of function f (x) = x + 6.
1. y = x + 6
2. x = y + 6
3. x - 6 = y which gives the inverse f -1 (x) = x - 6 |
Method 3 (graphing):
The graph of an inverse relation is the reflection of the original graph over the
line y = x (called the Identity Function). It may be necessary to restrict the domain of the starting function to ensure that the inverse is also a function.
Our starting function is y = 2x + 1.
If we reflect our starting function over the identity line, y = x, we obtain the red dotted line. The new red line is our inverse of y = 2x + 1.
For this example, the inverse passes the vertical line test, making the inverse a function.
Since this inverse is a straight line, we can easily find its equation. The inverse passes through (1,0) and (3,1) giving a slope of ½.
y - 0 = ½( x - 1) so, y = ½ (x - 1). |
|
The composition of a function with its inverse, will graphically yield the line y = x.
Remember:
f (f -1(x)) = x. |
| Determine graphically if an inverse is also a "function": |
We know that the Vertical Line Test is used to determine if a graph represents a function.
[ It states: If a vertical line drawn anywhere on a graph only intersects the graph in one location, the graph is a function.]
Horizontal Line Test:
If a horizontal line intersects the graph of a function, in all locations, at exactly one point, then the given function has an inverse that is also a function. The graph of the original function is said to "pass" the horizontal line test. |
To use the Horizontal Line Test:
Simply draw a horizontal line anywhere on the original function. Just like the Vertical Line Test, the horizontal lines must intersect the graph in only one location.
If there is only one intersection point, for every horizontal line, the graph has an inverse which is also a function.
If the original function passes the Horizontal Line Test, its inverse will pass the Vertical Line Test and also be a function.
This example verifies that the inverse of y = 2x + 1 will be a function.
|
|
| Restrict the domain to insure an inverse "function": |
If a horizontal line intersects the original graph in more than one location, it may be possible to restrict the domain of the original graph to ensure the inverse will be a function, and the original graph will pass the Horizontal Line Test for having an inverse function.
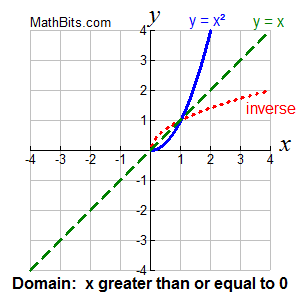
The parabola shown at the right is a function. You can see however that the reflection of the parabola (in red) over y = x does NOT form a function.
The Horizontal Line Test applied to the original parabola (in blue) would validate that the inverse will not be a function.
It is possible, however, to restrict the domain of the parabola y = x² to ensure that the inverse of a portion of the original graph will be a function. |
|
To restrict the domain, we want to cut the original function in such a way that what remains will pass the Horizontal Line Test ensuring the inverse to be a function.
Here are two possible restrictions which ensure that the inverse of y = x² will be a function for a portion of the graph. Since y = x² is a parabola, cutting the function at the turning point, (0,0), will work nicely.
Function: y = x² for x > 0
 |
Function: y = x² for x < 0
 |
|
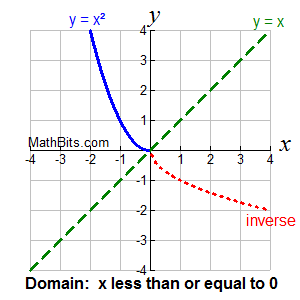