Transformations on Logarithmic Functions
 

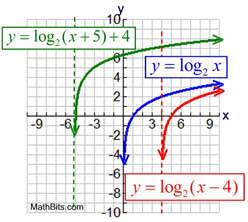
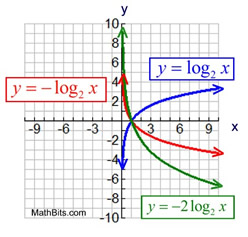
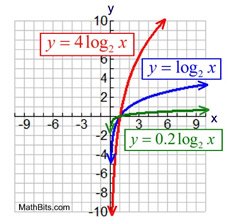
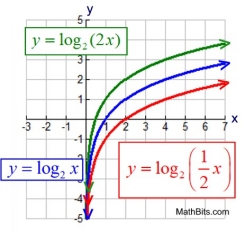
We know that transformations have the ability to move functions by sliding, reflecting, rotating, stretching, and shrinking them. Let's see how these changes will affect the logarithmic function:

Logarithmic Function   ylogb    Transformation Examples:
Translation
y = logb(x - h) + k
horizontal by h: vertical by k:

logtran
Domain: x > h
Range: x ∈ Real numbers

Translations:

Vertical Shift: f (x) + k

Horizontal Shift: f (x + h)


Reflections:

-f (x) over x-axis

f (-x) over y-axis
Reflection
y = a logbx
(a < 0) in x-axis:
logreflect
Domain: x > 0
Range: x ∈ Real numbers
Vertical Stretch/Compress
y = c logbx
 Stretch (|c| > 1):
Compress or Shrink
(0 < |c| < 1):
logstretch
Domain: x > 0
Range: x ∈ Real numbers

Vertical Stretch/Compress

c • f (x) stretch ( |c| > 1)

c • f (x) compress (0 < |c| < 1)

 

Horizontal Stretch/Compress

f (c • x) stretch (0 < |c| < 1)

f (c • x) compress ( |c| > 1)

 Horizontal Stretch/Compress
y = logb(cx)
Stretch (0 < |c| < 1):
Compress or Shrink
( |c| > 1):

Domain: x > 0
Range: x ∈ Real numbers

 

Overall formula for transformations of a logarithmic function,
from the parent   y = logb x   is:   y = a logb (c(x - h)) + k .

Note: The independent variable is x with the domain of real numbers.    

divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".