|
We know that a function is a set of ordered pairs in which no two ordered pairs that have
the same first component have different second components.
Given any x, there is only one y that can be paired with that x.
The following diagrams depict functions:
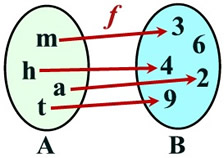 Function f:
Function f:
(m,3), (a,2), (t,9), (h,4)
|
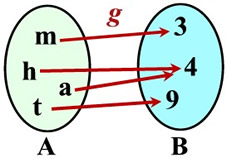 Function g: Function g:
(m,3), (a,4), (t,9), (h,4) |
In these diagrams, set A is the domain of the function and set B is the range of the function.
With the definition of a function in mind, let's take a look at some special "types" of functions.
One-to-One Functions
|
A function f from A to B is called one-to-one (or 1-1) if whenever f (a) = f (b) then a = b. No element of B is the image of more than one element in A.
|
|
In a one-to-one function, given any y value, there is only one x that can be paired with the given y.
Such functions are also referred to as injective.
 When working on the coordinate plane, a function is a one-to-one function when it will pass the vertical line test (to make it a function) and also a horizontal line test (to make it one-to-one). When working on the coordinate plane, a function is a one-to-one function when it will pass the vertical line test (to make it a function) and also a horizontal line test (to make it one-to-one). |
 Function f:
Function f:
One-to-One
Each y value that is used, is used only once.
|
 Function g: Function g:
NOT One-to-One
The y-value of 4 is used more than once.
|
When working in the coordinate plane, the sets A (the domain) and B (the range)
will most often both become the Real Numbers,
stated as 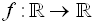 . .
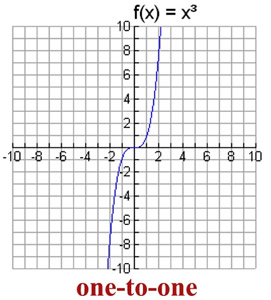
EXAMPLE 1: Is f (x) = x³ a one-to-one function where 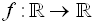 ? ? |
|
 |
This function is One-to-One. |
This cubic function is indeed a "function" as it passes the vertical line test. In addition, this function possesses the property that each x-value has one unique y-value that is not used by any other x-element. This characteristic is referred to as being a 1-1 function.
Notice that this function passes BOTH a vertical line test and a horizontal line test.
|
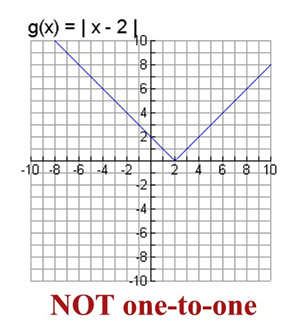
EXAMPLE 2: Is g (x) = | x - 2 | a one-to-one function where 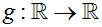 ? ? |
This function is
NOT One-to-One. |
 |
This absolute value function passes the vertical line test to be a function. In addition, this function has y-values that are paired with more than one x-value, such as (4, 2) and (0, 2). This function is not one-to-one.
This function passes a vertical line test
but not a horizontal line test. |
|
EXAMPLE 3: Is g (x) = | x - 2 | a one-to-one function where 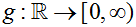 ? ? |
|  This question is changing the RANGE, not the DOMAIN. This question is changing the RANGE, not the DOMAIN.
It may be possible to adjust a function in some manner so that the function becomes a one-to-one function. In this case, with set B, the range, redefined to be 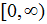 , function g (x) will still be NOT one-to-one since we still have (0,2) and (4,2). , function g (x) will still be NOT one-to-one since we still have (0,2) and (4,2).
There are restrictions on the DOMAIN that will create a one-to-one function in this example. For example, restricting A, the domain, to be only values from -∞ to 2 would work, or restricting A, the domain, to be only elements from 2 to ∞ would work. Notice that restriction A, the domain, to be 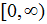 would NOT create a one-to-one function as we would still have (0,2) and (4,2). would NOT create a one-to-one function as we would still have (0,2) and (4,2). |

Onto Functions
|
A function f from A to B is called onto if for all b in B there is an a in A such that whenever f (a) = b. All elements in B are used.
|
|
Keep in mind that in an onto function, all possible y-values are used.
Such functions are also referred to as surjective.
 Function f:
Function f:
Onto
All elements in B are used.
Not one-to-one.
|

Function f:
NOT Onto
The 6 in B is not used.
It is one-to-one. |
To determine if a function is onto, you need to know information about both set A and set B.
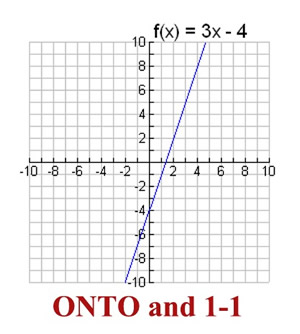
EXAMPLE 1: Is f (x) = 3x - 4 is an onto function where 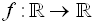 ? ? |
|
|
This function
(a straight line)
is ONTO. |
As you progress along the line,
every possible y-value is used.
In addition, this straight line also possesses the property that each x-value has one unique y-value that is not used by any other x-element. This function is also one-to-one.
|
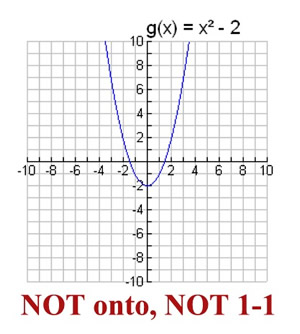
EXAMPLE 2: Is g (x) = x² - 2 an onto function where 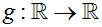 ? ? |
This function
(a parabola)
is NOT ONTO. |
 |
Values less than -2 on the y-axis are never used. Since only certain y-values belonging to the set of ALL Real numbers are used, we see that not ALL possible y-values are used.
Note that in addition, this parabola also has y-values that are paired with more than one x-value,
such as (3, 7) and (-3, 7).
This function will not be one-to-one. |
|
EXAMPLE 3: Is g (x) = x² - 2 an onto function where 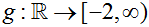 ? ?
If set B, the range, is redefined to be 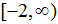 , ALL of the possible y-values are now used, and function g (x) under these conditions) is ONTO. Note that this function is still NOT one-to-one. , ALL of the possible y-values are now used, and function g (x) under these conditions) is ONTO. Note that this function is still NOT one-to-one.
To make this function both onto and one-to-one, we would also need to restrict A, the domain. |

BOTH
1-1 &
Onto Functions
|
A function f from A (the domain) to B (the range) is BOTH one-to-one and onto when no element of B is the image of more than one element in A, AND all elements in B are used.
|
|
Functions that are both one-to-one and onto are referred to as bijective.
Bijections are functions that are both injective and surjective.
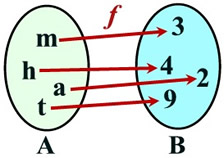
Function f:
BOTH
One-to-one and
Onto
Each used element of B is used only once, and All elements in B are used.
|
 Function f: Function f:
NOT BOTH
One-to-one, NOT onto
Each used element of B is used only once, but the 6 in B is not used. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|