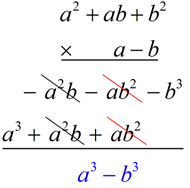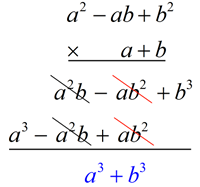In Algebra 1, you worked with factoring the difference of two perfect squares.
a² - b² = (a - b)(a + b)

The sum of two perfect squares, a2 + b2, does not factor under Real numbers.

In Algebra 2, we will extend our factoring skills
to factoring BOTH the difference and the sum of two perfect CUBES.

Factor the Difference of Perfect Cubes:

a3 - b3 = (a - b)(a2 + ab + b2)

Factor the Sum of Perfect Cubes:

a3 + b3 = (a + b)(a2 - ab + b2)

Let's see that these formulas are actually true.

Check a3 - b3 formula:

Check a3 + b3 formula:

There is a pattern to the "signs" in the factored form.

Remember the Factored Pattern:

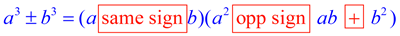
• the first binomial term keeps the same sign as the sign between the perfect cubes. • the sign separating the first and second terms of the trinomial is opposite the sign between the perfect cubes • the last sign in the trinomial is always positive. (Note that each formula has only one negative sign in the solution.)

If all else fails, you can find the factored trinomial by using long division.

One more idea for remembering these patterns: If you remember one of the patterns,
you can obtain the other pattern by substituting "-b" in place of "b" in your known pattern.
For example, if you know:   a³ + b³ = (a + b)(a² - ab + b²)
Replace b with -b:   a³ + (-b)³ = (a + (-b))(a² - a(-b) + (-b)²)
and you have:    a³ - b³ = (a - b)(a² + ab + b²)

Let's look at how the "terms" are related.

When working with perfect cubes look for: perfect cube numerical values: 8, 27, 64, 125, 216, 343, 512, ... powers for perfect cube algebraic values: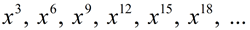

Notice the placement of the "x" and the "numerical entries".

Factor: x3 - 125 = (x - 5)(x2 + 5x + 25) = (x - 5)(x2 + 5x + 52)

Factor: x3 - 343 = (x - 7)(x2 + 7x + 49) = (x - 7)(x2 + 7x + 72)

Factor: x3 - a3 = (x - a)(x2 + ax + a2)

Factor: x3 + 125 = (x + 5)(x2 - 5x + 25) = (x + 5)(x2 - 5x + 52)

Factor: x3 + 343 = (x + 7)(x2 - 7x + 49) = (x + 7)(x2 - 7x + 72)

Factor: x3 + a3 = (x + a)(x2 - ax + a2)

This pattern will be helpful when trying to identify whether an expression
might be the quadratic trinomial component of a perfect cube.

	Factor: 8x3 - 27
Is this expression the difference of perfect cubes? Look for perfect cubes and appropriate powers. 8x3 and 27 are perfect cubes: 8x3 = (2x)3 and 27 = 33 So, yes, this is the difference of perfect cubes.	(2x)3 - 33 a = 2x, b = 3
Use formula: a3 - b3 = (a - b)(a2 + ab + b2). Be sure to use parentheses to avoid problems.	(2x - 3)((2x)2 + (2x)(3) + 32)
Remove the inner parentheses on the trinomial expression. This is your factored answer.	(2x - 3)(4x2 + 6x + 9)

	Factor: 64x9 + 125
64x9 = (4x3)3 and 125 = 53 This expression is the sum of perfect cubes.	(4x3)3 + 53
a = 4x3 and b = 5 formula: a3 + b3 = (a + b)(a2 - ab + b2)	(4x3 + 5)((4x3)2 - (4x3)(5)+ 52)
Simplify the trinomial to get the factored form.	(4x3 + 5)(16x6- 20x3+ 25)

	Factor: 56m3 - 7n3
At first glance, this may not look like the difference of perfect cubes. BUT, if we factor out the common factor of 7, we will find a hidden difference of perfect cubes.	7(8m3 - n3)
a = 2m and b = n Use formula: a3 - b3 = (a - b)(a2 + ab + b2).	7(2m - n)((4m)2 + 2mn + n2)
Solution:	7(2m - n)(4m2 + 2mn + n2)

There is also an observable pattern to "cubing binomials":
Remember: (x + a)³ is NOT (x³ + a³)

Cubing a binomial:

(x + a)3 = x3 + 3ax2 +3a2x + a3

You can obtain this next pattern by substituting "-a" for "a":

(x - a)3 = x3 - 3ax2 +3a2x - a3

When you work with the Binomial Theorem, you will get a better understanding
of this pattern of the coefficients in these formulas.

Remember: you can always find these patterns by simply multiplying
(x + a)³ = (x + a)(x + a)( x + a)
(x - a)³ = (x - a)(x - a)( x - a)