|
 |
Shape: Smooth and
continuous, no holes, breaks, or sharp turns. |
Parent Functions:
(Note: These parent functions are also "power" functions)
Degree 2 - Quadratic
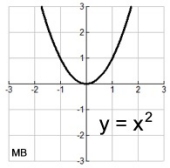 |
Degree 3 - Cubic
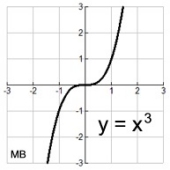 |
Degree 4 - Quartic
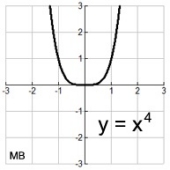 |
Degree 5 - Quintic
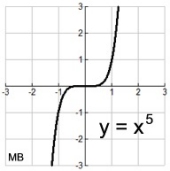 |
| End Behavior: |
Functions of EVEN POWERS w/
leading coefficients positive:
as x → + ∞, f (x) → + ∞
as x → - ∞, f (x) → + ∞
Both ends point up. |
Functions of EVEN POWERS w/
leading coefficients negative:
as x → + ∞, f (x) → - ∞
as x → - ∞, f (x) → - ∞
Both ends point down. |
| |
Functions of ODD POWERS w/
leading coefficients positive:
as x → + ∞, f (x) → + ∞
as x → - ∞, f (x) → - ∞
Left end points down, right end up. |
Functions of ODD POWERS w/
leading coefficients negative:
as x → + ∞, f (x) → - ∞
as x → - ∞, f (x) → + ∞
Left end points up, right end down. |
| Equation Form: |
y = anxn + an - 1xn - 1 + . . . + a2x2 + a1x + a0
Non-negative integer exponents. Coefficients are real numbers.
Degree is the highest power. Leading term has the highest degree.
|
Roots/Zeros:
|
Maximum number of x-intercepts (zeros) = the degree.
Odd degree polynomials have at least one x-intercept (zero).
Even degree polynomials may have no x-intercepts (zero).
Complex roots appear in conjugate pairs.
Multiplicity: number of times a root repeats.
Odd multiplicity = graph crosses the x-axis at that root.
Even multiplicity = graph only touches the x-axis at that root (no crossing). |
Graph
characteristics: |
Domain: all Real numbers.
Range: depends upon the degree.
Every polynomial function has exactly one y-intercept, f (0).
Maximum number of turning points = the degree - 1.
"Turning points" may also be called "local maxima" or "local minima",
or called "relative maxima" or "relative minima".
Maximum/Minimum: All polynomial functions of EVEN degree have an "absolute" maximum or "absolute" minimum. ("Absolute" max/min is the greatest/least value attained by the function over its domain.) |
Symmetry:
|
Most polynomial functions have no symmetrical properties.
Those that are symmetric with the y-axis will most likely be
"even functions" where f (-x) = f (x).
Those that are symmetric about the origin will most likely be
"odd functions" where f (-x) = -f (x).
Do not confuse a polynomial of even degree with an even function. |
Polynomial Function - Possible Real Roots and Complex Roots:
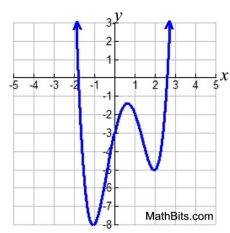 DEGREE 4:
DEGREE 4:
y = x4 - 2x3 - 3x2 +5x - 3
Calculator: roots at (-1.8,0) and (2.6,0) with two complex roots. |
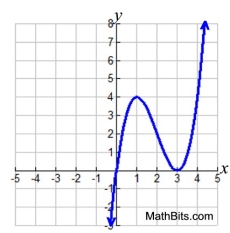 DEGREE: 3
DEGREE: 3
y = x(x - 3)2
Multiplicity of ( x - 3) is 2.
Graph only touches x-axis at x = 3. |
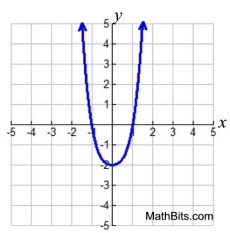 DEGREE 4:
DEGREE 4:
y = x4 + x2 - 2
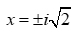 ,1 -1,
|
Polynomial Function - Transformation Examples:
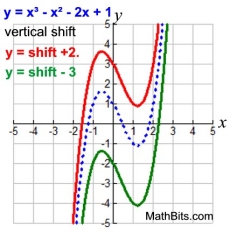 Translations
Translations
|
Translations:
Vertical Shift: f (x) + k
Horizontal Shift: f (x + k)
Reflections:
-f (x) over x-axis
f (-x) over y-axis
|
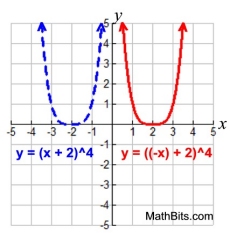
Reflection |
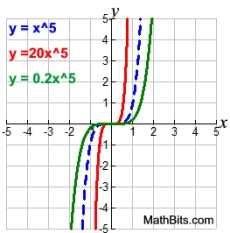
Vertical Stretch/Compress |
Vertical Stretch/Compress
k • f (x) stretch (k > 1)
k • f (x) compress (0 < k < 1)
Horizontal Stretch/Compress
f (k • x) stretch (0 < k < 1)
f (k • x) compress ( k > 1) |
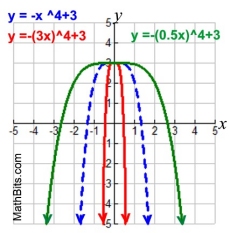
Horizontal Stretch/Compress |
The carrot symbol, ^, can be used to denote exponent. Example: x³ = x^3.
This can be helpful when the size of the exponeent becomes hard to read in extremely small print.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|












