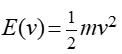|
Power functions were first mentioned during the discussion of exponents.
Now, we'll take a closer look, and see how "power functions"
play a role in dealing with polynomial functions.

But first, let's become better acquainted with power functions.
 |
A power function is a function with a single term where a variable is raised to a constant power, written in the form f (x) = kxp where k is a |
| non-zero constant coefficient and p is any real number exponent (i.e., the "power"). |
|
You may see a definition that limits k to be equal to only 1, but the definition above is more common.
Since p is allowed to be any real number, there is a wide range
of possible power functions. Here are a few possible power functions:
Some of these are "Parent functions:
• constant function: f (x) = x0 = 1
• identity function: f (x) = x1 = x
• reciprocal function: f (x) = x-1 =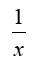
• square root function: f (x) = x½ = 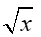
• quadratic function: f (x) = x2 |
Known formulas that are power functions:
• area of a circle: 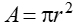
• volume of sphere: 
• kinetic energy: 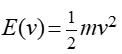
(v = velocity for a constant mass, m)
|
We will be concentrating on a connection between power functions and polynomial functions.
As such, we will be limiting power functions to exponents that are whole numbers
to coincide with the exponent limitations of polynomials.

Let's examine the graphs of "even" power functions:
f (x) = kxp
where p is an "even" positive integer:
Notice: x is the variable, while k and p are constants (which do not change as x changes).
Graph: ("even" powers, k positive)
f (x) = x2
f (x) = x4
f (x) = x6
From the graph, it can be seen that these even powers create a somewhat parabolic shape (a strange looking letter U).
For these even powers, all results are positive, including the negative x-values which become positive when squared (or raised to the powers of 4, 6, ...).
|
These 3 graphs intersect with one another at the points (-1,1) and at (1,1).
A horizontal line drawn through these two points will show a change in behavior of the graphs.
• Below the line, the larger powers lie below the smaller powers.
• Above this line, the larger powers lie above the smaller powers.
All of these graphs pass through the origin. |
|
Notice both ends of the even power graphs pointing upward (and k is positive).
Power Function End Behavior: (even power, k = positive)
If the coefficient is positive, the end behavior approaches positive infinity in both horizontal directions (both ends up).
x → +∞, f (x) → +∞
x → -∞, f (x) → +∞
|
Remember: The "end behavior" refers to the appearance of a graph as it is followed indefinitely in either horizontal direction.
|
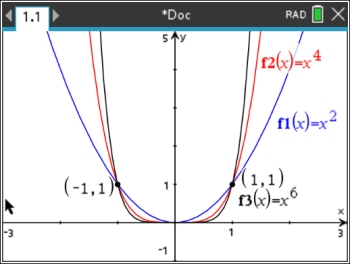
This second graph (at the right) shows the reflection of the even power functions over the x-axis.
Graph: ("even" powers, k negative)
f (x) = -x2
f (x) = -x4
f (x) = -x6
Remember: This negation is -x2 and not (-x)2.
The graph maintains its somewhat parabolic shape (an odd upside down letter U).
Since all of the applications of the even powers are being negated, all of the y-values are negative (except for the origin). All of these graphs pass through the origin. |
This graph resembles the previous graph in shape, size, and characteristics. As the reflection, however, the graph is "pointing" downward, instead of upward. |
|
Notice both ends of negated even power graphs are pointing downward (and k is negative).
Power Function End Behavior: (even power, k = negative)
If the coefficient is negative, the end behavior approaches negative infinity in both horizontal directions (both ends down).
x → +∞, f (x) → -∞
x → -∞, f (x) → -∞
|

|
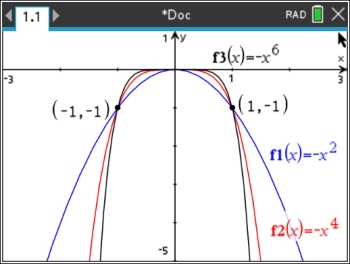
Let's examine the graphs of "odd" power functions:
f (x) = kxp
where p is an "odd" positive integer:
Graph: ("odd" powers, k positive)
f (x) = x3
f (x) = x5
f (x) = x7
From the graph, it can be seen that odd powers create a different shape than "even" powers.
Odd powers allow for a negative
x-value to create a negative result (i.e., cubing a negative x-value gives a negative result). So, when x is negative, the y-values are negative in the 3rd quadrant.
|

These 3 graphs intersect with one another at the points (-1,-1) and at (1,1).
• In the first quadrant, the "odd" graphs take on a look and characteristics much like those of the "even" functions in quadrant one.
• In the third quadrant, the "odd" functions take on a look and characteristic much like those of the reflection over the x-axis for the 2nd quadrant "even" values.
All of these graphs pass through the origin.
|
|
Notice both ends of the odd power graphs pointing in different directions (and k is positive).
Power Function End Behavior: (odd power, k = positive)
If the coefficient is positive, the end behavior approaches negative infinity at the far left, and positive infinity at the far right. (left down, right up).
x → +∞, f (x) → +∞
x → -∞, f (x) → -∞
|
| |
| This second graph (at the right) shows the reflection of the odd power functions over the x-axis.
Graph: ("odd" powers, k negative)
f (x) = -x3
f (x) = -x5
f (x) = -x7
Remember: This negation is -x3 and not (-x)3.
The graph maintains its same shape, but as a reflection of the previous graph.
Since all of the applications of the odd powers are being negated, the y-values that were previously negative have become positive and vice versa (except for the . origin). All of these graphs pass through the origin. |
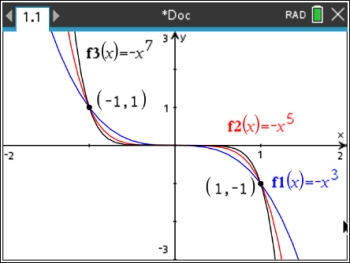
This graph resembles the previous graph in shape, size, and characteristics. As the reflection, however, the graph is now pointing up on the left, and down on the right. |
|
|
Power Function End Behavior: (odd power, k = negative)
If the coefficient is negative, the end behavior approaches positive infinity at the far left, and negative infinity at the far right. (left up, right down).
x → +∞, f (x) → -∞
x → -∞, f (x) → +∞
|
|
|

f (x) = kxp
The end behaviors for power functions are:
even powers - both ends in the same direction
k positive = both up
k negative = both down
odd powers - ends in opposite directions
k positive = left down, right up
k negative = left up, right down. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|