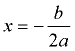|
 Shape: Parabola Shape: Parabola
 Symmetric about the y-axis.
Turning point (minimum) at (0,0). Symmetric about the y-axis.
Turning point (minimum) at (0,0). |
Equation Forms:
• Vertex Form:
y = a(x - h)2 + k
with
vertex (h,k)
easy access to finding vertex, max/min, inc/dec
• Point-Slope Form:
y = ax2 + bx + c
shows general form of graph and roots (zeros)
• Intercept Form:
y = a( x - p)( x - q)
p and q are x-intercepts.
shows roots, pos/neg
|
|
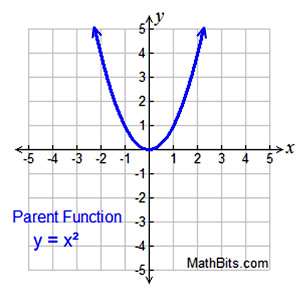
Axis of Symmetry:
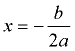 locates "turning point"
locates "turning point"
(vertex)
Average rate of change
NOT constant
x-intercept(s):
determine roots/zeros
y-intercept:
(0, y) |
| End Behavior: |
Parent Function: f (x) = x²
as x → + ∞, f (x) → + ∞
as x → - ∞, f (x) → + ∞
parabola opens upward |
Negative Coefficient: f (x) = -x²
as x → + ∞, f (x) → - ∞
as x → - ∞, f (x) → - ∞
parabola opens downward
|
The quadratic function y = x2 is an even function: f (-x) = f (x) |
Quadratic Function - Possible Real Roots and Complex Roots:
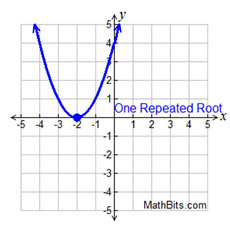 y = (x + 2)(x + 2)
y = (x + 2)(x + 2)
x = -2; x = -2
Repeated root
Multiplicity 2 |
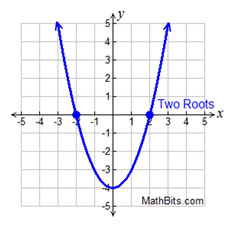 y = (x - 2)(x + 2)
y = (x - 2)(x + 2)
x = 2; x = -2
Each root is
multiplicity 1 |
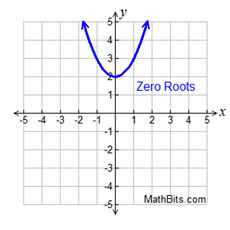 y = x² + 2
y = x² + 2
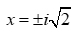
roots are complex (imaginary) |
Maximum/Minimum: Finding the "turning point" (vertex) will locate the maximum or minimum point. The intervals of increasing/decreasing are also determined by the vertex.
Quadratic Function - Transformation Examples:
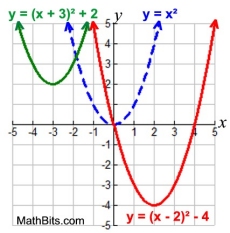 Translations
Translations |
Translations:
Vertical Shift: f (x) + k
Horizontal Shift: f (x + k)
Reflections:
-f (x) over x-axis
f (-x) over y-axis
|
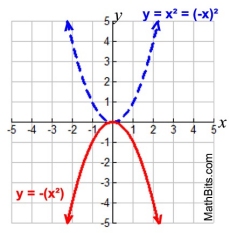
Reflection |
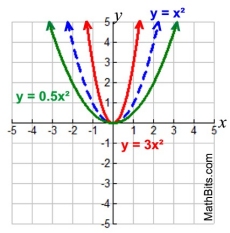
Vertical Stretch/Compress |
Vertical Stretch/Compress
k • f (x) stretch (k > 1)
k • f (x) compress (0 < k < 1)
Horizontal Stretch/Compress
f (k • x) stretch (0 < k < 1)
f (k • x) compress ( k > 1) |
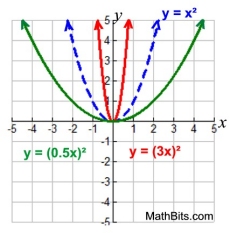
Horizontal Stretch/Compress |
Remember: for y = ax2 + bx + c, negative "a" opens down.

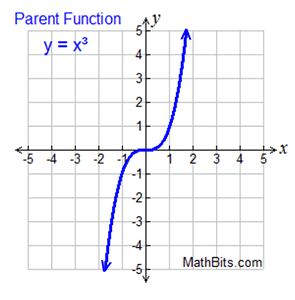 Cubic functions are of degree 3.
Cubic functions are of degree 3. |
Example Equation Forms:
• y = x3
(1 real root - repeated)
• y = x3- 3x2= x2(x - 3)
(two real roots - 1 repeated)
• y = x3+2x2+x = x(x + 1)2
(three visible terms)
• y = x3+3x2+3x+1=(x+1)3
(1 real root - repeated)
• y = (x+1)(x - 2)(x - 3)
(factored form - 3 real roots) |
|
Symmetric (for y = x³):
about origin
Average rate of change:
NOT constant
x-intercept(s):
determine roots/zeros
y-intercept:
(0, y)
End Behavior:
One end approaches +∞,
other end approaches -∞.
(Unless domain is altered.)
|
| End Behavior: |
Parent Function: f (x) = x³
as x → + ∞, f (x) → + ∞
as x → - ∞, f (x) → - ∞
left points down, right points up |
Negative Coefficient: f (x) = -x³
as x → + ∞, f (x) → - ∞
as x → - ∞, f (x) → + ∞
left points up, right points down |
The cubic function y = x3 is an odd function: f (-x) = -f (x) |
Cubic Function - Possible Real Roots:
 y = x³
y = x³
1 Real Root (repeated) |
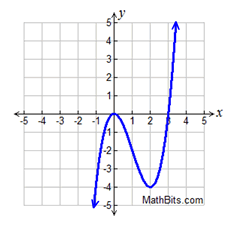 y = x³ - 3x²
y = x³ - 3x²
2 Real roots (1 repeated) |
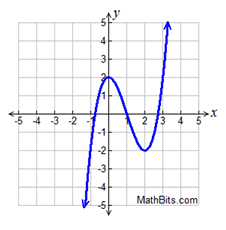 y = x
y = x³ - 3 x² + 2
3 Real roots |
Note: The cubic function will always cross the x-axis at least once, so there will always be at least one real root.
Cubic Function - Transformation Examples:
 Translations
Translations |
Translations:
Vertical Shift: f (x) + k
Horizontal Shift: f (x + k)
Reflections:
-f (x) over x-axis
f (-x) over y-axis
|
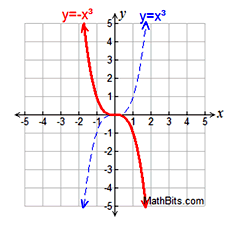
Reflection |
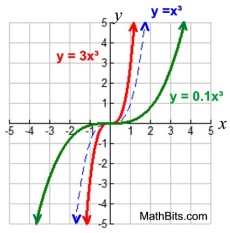
Vertical Stretch/Compress |
Vertical Stretch/Compress
k • f (x) stretch (k > 1)
k • f (x) compress (0 < k < 1)
Horizontal Stretch/Compress
f (k • x) stretch (0 < k < 1)
f (k • x) compress ( k > 1) |
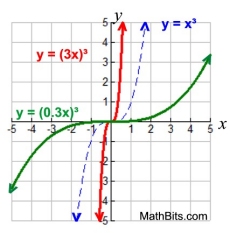
Horizontal Stretch/Compress |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|