 |
Quadratic: Involving terms of the second degree at most.
Parabolas (y = x2 - 4x - 2) and circles (x2 + y2 = 16) are quadratics.
|
|
A linear quadratic system is a system containing one linear equation and one quadratic equation.
Linear-Quadratic System
Line - Parabola
y = x - 2
y = x2 - 4x - 2 |
Linear-Quadratic System
Line - Circle
2y = x +1
x2 + y2 = 1
|
Algebra 1 focused on linear-quadratic systems that contained straight lines and parabolas.
Algebra 2 will work with linear-quadratic systems containing straight lines and parabolas,
but the emphasis will be on linear-quadratic systems containing straight lines and circles.

REFRESH:
Linear-Quadratic System: linear equation and parabola
(only one variable is squared) |
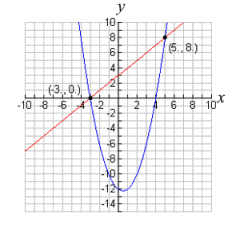
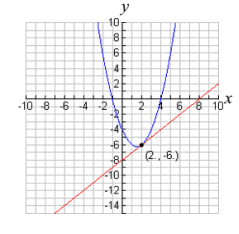
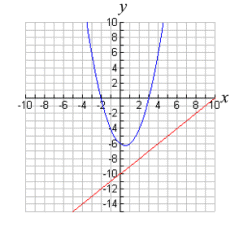
This familiar linear-quadratic system, has only one variable being squared, and will be the graph of a straight line and a parabola. The graphs below show that when a line and a parabola are graphed on the same set of axes, three situations are possible.
 |
 |
 |
| The equations will intersect in two locations.
Two real solutions. |
The equations will intersect in one location. One real solution. |
The equations will not intersect.
No real solutions. |
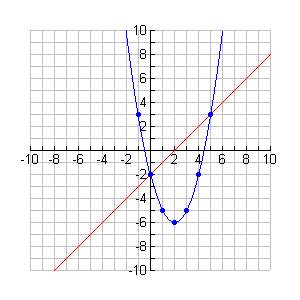
Find the intersection points for a linear quadratic (parabola) system algebraically:
Algebraic Solution:
Solve:
y = x - 2
y = x2 - 4x - 2
Solution:
{(0,-2), (5,3)}
|
We will be substituting the
"y =" from the second equation
for the
"y =" value of the first equation.
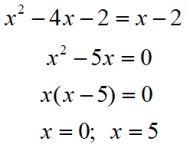
|
The x-coordinates of the solutions will be 0 and 5.
(0, __) and (5, __)
Find the missing y-values:
y = 0 - 2
y = -2
(0,-2)
y = 5 - 2
y = 3
(5,3) |
To check, substitute the coordinates for each solution into both equations.
Graphical
Solution:

By hand:
Solve by graphing:
y = x - 2
y = x2 - 4x - 2
To check: place the solution coordinates into each equation. |
Use axis of symmetry to establish the turning point for the parabola:
x = -b/2a = -(-4)/2(1) =2
x = 2 turning point at (2,-6)
Use (2,-6) as middle of the table.
| x |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
| y |
3 |
-2 |
-5 |
-6 |
-5 |
-2 |
3 |
Use y = mx + b for line graph.
m = 1, and b = -2
Solution: {(0,-2), (5,3)} |
 |
In the Example above, we were lucky in that the intersection points gave us integer coordinates.
That is not always the case.
In Algebra 2, a graphical solution will rely on the graphing calculator to arrive at a solution,
since integer solutions will be seen less often.

By calculator:
Solve by graphing:
y = x - 2
y = x2 - 4x - 2
Solution:
{(0,-2), (5,3)} |
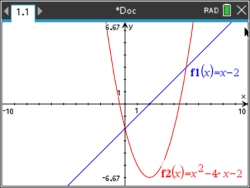
Graph the equations.
f 1(x) = x - 2
f 2(x) = x2 - 4x - 2
Be sure your viewing window shows a clear picture of the parabola and the line.
 |
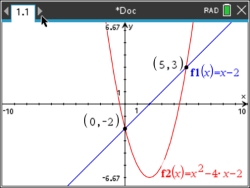
Use the INTERSETION option twice to find the two locations where the graphs intersect.
MENU #6 #4
The intersection points appear
as (0,-2) and (5,3).
|

Linear-Quadratic System: linear equation and circles
(both variables are squared) |
Let's take a look at a linear-quadratic system, having two variables squared,
where one equation is a line and the other is a circle.
Like with the parabola, the graphs below show that when a line and a circle are graphed on the same set of axes, three situations are possible.
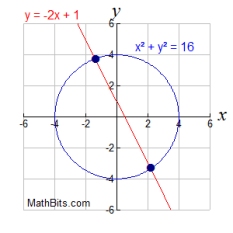 |
 |
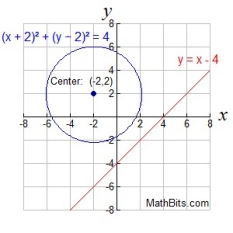 |
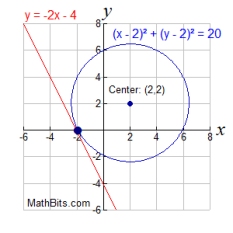
| The equations will intersect in two locations.
Two real solutions. |
The equations will intersect in one location (a tangent). One real solution. |
The equations will not intersect.
No real solutions. |
Find the intersection points for a linear quadratic (parabola) system algebraically:
Algebraic Solution:
Solve:
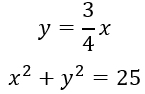
We will be substituting the "y =" value into the second equation to solve for x.
Solution:
{(-4,-3), (4,3)}
|
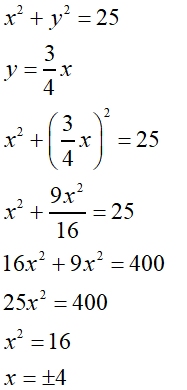 |
The x-coordinates of the solutions will be +4 and - 4.
(4, __) and (-4, __)
Find the missing y-values by substituting the +4 and -4. 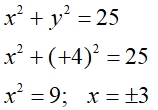
The result is the same for both +4 and -4.
We know, from the graph, that the x = -4 is in the third quadrant, so we have
(-4,-3).
And likewise, since the x = +4 is in the first quadrant, we have (4,3). |
Graphical
Solution:
By hand:
Solve by graphing:
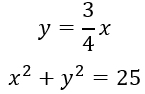
|
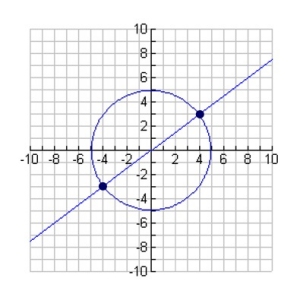
This circle has a center at the origin with a radius of 5.
Use y = mx + b for line graph.
m = ¾, and b = 0.
Solution: {(-4,-3), (4,3)}
To check: place the solution coordinates into each equation. |
 |

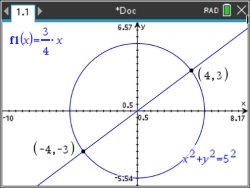
By calculator:
Solve by graphing:
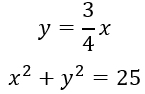
Solution:
{(-4,-3), (4,3)} |
For calculator help graphing
a circle, see
Graphing Circle Equations.
Graph the equations.
f 1(x) =¾ x
f 2(x) = x2 + y2 = 25
Hint: graph the line first.
Be sure your viewing window shows a clear picture of the circle and the line.
|
Use the INTERSETION option twice to find the two locations where the graphs intersect.
MENU #6 #4
The interest option will create a box surrounding the intersection point.
Click once to lock a corner of the box, then drag to form the box.
|
|