We saw an introduction to the concept of "end behavior" of a graph in Algebra 1.
Specifically, we saw the following charts regarding "end behavior" for quadratic functions.
Leading coefficient POSITIVE:
both "ends" point UP. 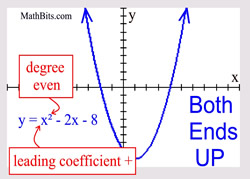 |
Leading coefficient NEGATIVE:
both "ends" point DOWN. 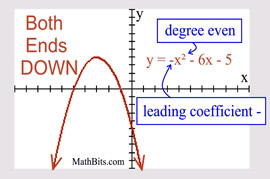
|
In Algebra 2, we would like to spiff up this information with a bit more precision and depth.
We know that quadratics are a subset of the polynomials. As such, the restrictions placed on "end behavior" for quadratics falls under the restrictions for "end behavior" placed on polynomials.
We will discover in the next unit that "end behavior" in polynomials
is determined by examining two conditions:
•
whether the polynomial's DEGREE is odd or even, and
• whether the LEADING COEFFICIENT is positive or negative.
The nice feature of working with Quadratics, is that they all have a degree of two, which is even.
There will be no need to examine the "degree" when working with quadratics. YEA!!
All we need to do is examine whether the leading coefficient is positive or negative.

Let's formalize the definition of "end behavior" a bit more.
 |
The "end behavior" of a polynomial function describes how the graph behaves as the x-variable (input) approaches positive infinity (x → +∞) and approaches negative infinity (x → -∞). (i.e., the "ends" of the graph) |
|
As pointed out above, determining "end behavior" for quadratics is a simple process:
• If the sign of the leading coefficient is positive,
the parabola opens upward (both ends point up).
x → +∞, f (x) → +∞
x → -∞, f (x) → +∞
• If the sign of the leading coefficient is negative,
the parabola opens downward (both ends point down).
x → +∞, f (x) → -∞
x → -∞, f (x) → -∞
As will be discussed further in the next unit, the "end behavior" of the quadratic
is being dominated by the behavior of its leading term.
In a quadratic function, y = ax2 + bx + c, as the | x | gets VERY, VERY big, (positively or negatively), the leading term, ax2, dominates the other two terms. Due to this dominance, the function behaves as if it was simply the power function y = ax2, and mimics the end-behavior of that power function.


